Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z

Bài 1: Số phức

Haylamdo biên soạn và sưu tầm lời giải Bài 9 trang 190 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 9 (trang 190 sgk Giải Tích 12 nâng cao): Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều kiện sau:

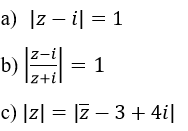
Lời giải:

a) Giả sử z=a+bi => z – I = a+(b-1)i

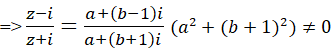
Vậy quỹ tích điểm M(a; b) biểu diễn số phức z=a+bi thõa mãn |z – i| =1 là đường tròn tâm I(0; 1), bán kính R = 1.

b) Giả sử z=a+bi

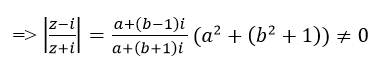
Theo bài 8b ta có:

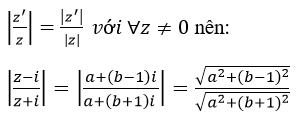
Theo bài ra ta có:

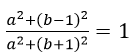
<=> a²+(b-1)²=a²+(b+1)²

<=> b = 0. Vậy z = a, hay tập hợp các điểm cần tìm là trục thực

c) Giả sử z=a+bi => z−=a-bi z−-3+4i=a-bi-3+4i=(a-3)+(4-b)i

Theo bài ra, ta có |z|=|z−-3+4i|<=> |z|=|(a-3)+(4-b)i|

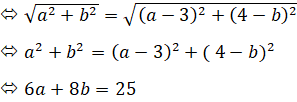
Vật quỹ tích điểm các điểm cần tìm trêm đường thẳng có phương trình 6x + 8y = 25 trong mặt phẳng phức (Oxy)