Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau

Toán lớp 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 4 (trang 44 SGK Giải tích 12): Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:

a) x³ - 3x² + 5 = 0 ;

b) -2x³ + 3x² - 2 = 0 ;

c) 2x² - x⁴ = -1

Lời giải:

a) Xét y = f(x) = x³ - 3x² + 5 (1)

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

f'(x) = 3x² - 6x = 3x(x - 2)

f'(x) = 0 ⇔ x = 0 ; x = 2

+ Giới hạn:

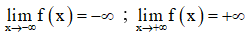
+ Bảng biến thiên:

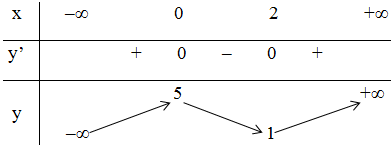
- Đồ thị:

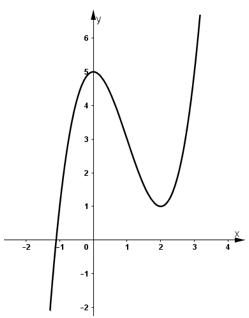
Đồ thị hàm số y = f(x) cắt trục hoành tại 1 điểm duy nhất.

⇒ phương trình x³ - 3x² + 5 = 0 chỉ có 1 nghiệm duy nhất.

b) Xét hàm số y = f(x) = -2x³ + 3x² – 2.

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

y' = -6x² + 6x = -6x(x - 1)

y' = 0 ⇔ x = 0 ; x = 1

+ Giới hạn:

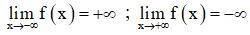
+ Bảng biến thiên:

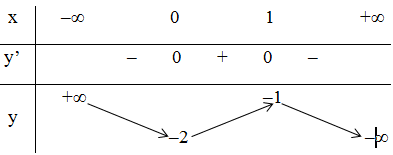
- Đồ thị:

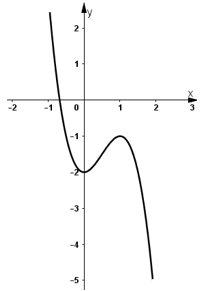
Đồ thị hàm số y = f(x) cắt trục hoành tại 1 điểm duy nhất

⇒ phương trình f(x) = 0 có nghiệm duy nhất.

Vậy phương trình -2x³ + 3x² - 2 = 0 chỉ có một nghiệm.

c) Xét hàm số y = f(x) = 2x² - x4

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

y' = 4x - 4x³ = 4x(1 - x²)

y' = 0 ⇔ x = 0 ; x = ±1

+ Giới hạn:

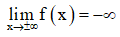
+ Bảng biến thiên:

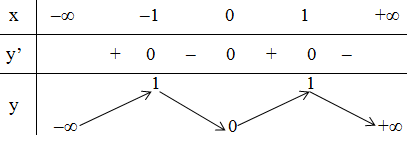
- Đồ thị:

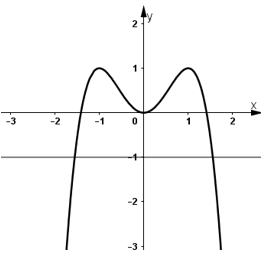
Đồ thị hàm số y = f(x) cắt đường thẳng y = -1 tại hai điểm

⇒ Phương trình f(x) = -2 có hai nghiệm phân biệt.

Kiến thức áp dụng