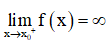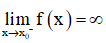Cho hàm số Chứng minh rằng với mọi giá trị của tham số m

Toán lớp 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 6 (trang 44 SGK Giải tích 12): Cho hàm số

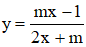
a) Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên khoảng xác định của nó.

b) Xác định m để tiệm cận đứng của đồ thị đi qua A(-1, √2).

c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.

Lời giải:

a) Với mọi tham số m ta có :

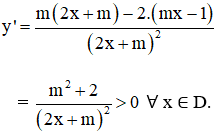
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

b) Ta có:

⇒ là tiệm cận đứng của đồ thị hàm số.

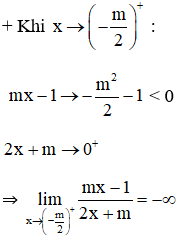
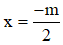
+ Tiệm cận đứng đi qua A(-1 ; √2)

⇔

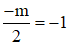
⇔ m = 2.

Vậy với m = 2 thì tiệm cận đứng của đồ thị đi qua A(-1, √2)

c) Với m = 2 ta được hàm số: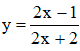

- TXĐ: D = R \ {-1}

- Sự biến thiên:

+ Chiều biến thiên: Theo kết quả câu a)

Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞)

+ Cực trị : Hàm số không có cực trị.

+ Tiệm cận:

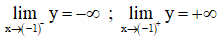
⇒ đồ thị có tiệm cận đứng là x = -1.

Lại có

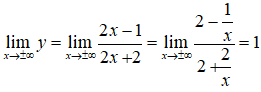
⇒ đồ thị có tiệm cận ngang là y = 1.

+ Bảng biến thiên:

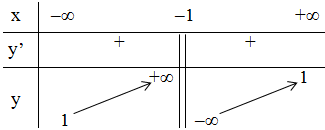
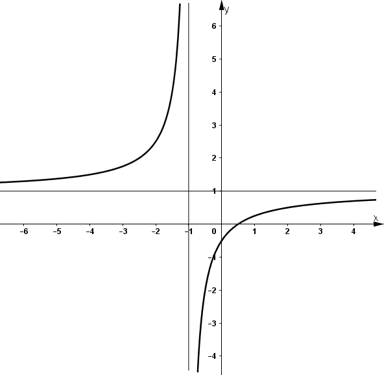
- Đồ thị:

+ Đồ thị cắt trục hoành tại (1/2 ; 0).

+ Đồ thị cắt trục tung tại (0 ; -1/2).

+ Đồ thị nhận I(-1 ; 1) là tâm đối xứng.

Kiến thức áp dụng