Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = -x3 + 3x + 1

Toán lớp 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 5 (trang 44 SGK Giải tích 12): a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:

y = -x³ + 3x + 1

b) Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m:

x³ - 3x + m = 0

Lời giải:

a) Khảo sát hàm số y = -x³ + 3x + 1

- Tập xác định: D = R

- Sự biến thiên:

+ Chiều biến thiên:

y' = -3x² + 3 = -3(x² - 1)

y' = 0 ⇔ -3(x² - 1) = 0 ⇔ x = ±1.

+ Giới hạn:

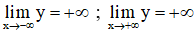
+ Bảng biến thiên:

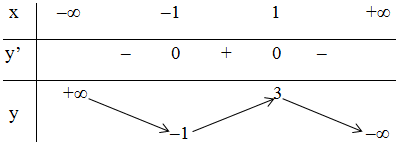
Kết luận: hàm số đồng biến trên khoảng (-1; 1).

hàm số nghịch biến trên các khoảng (-∞; -1) và (1; +∞).

Hàm số đạt cực tiểu tại x = -1 ; y_CT = -1.

Hàm số đạt cực đại tại x = 1 ; y_CĐ = 3.

- Đồ thị:

+ Giao với Oy: (0; 1).

+ Đồ thị (C) đi qua điểm (-2; 3), (2;-1).

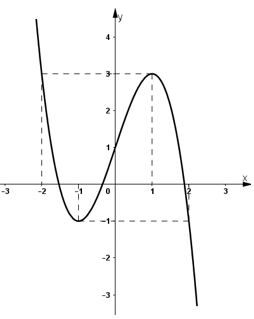
b) Ta có: x³ - 3x + m = 0 (*)

⇔ -x³ + 3x + 1 = m + 1

Số nghiệm của phương trình (*) phụ thuộc số giao điểm của đồ thị hàm số y = -x³ + 3x + 1 và đường thẳng y = m + 1.

Kết hợp với quan sát đồ thị hàm số ta có :

+ Nếu m + 1 < –1 ⇔ m < –2

⇒ (C ) cắt (d) tại 1 điểm.

⇒ phương trình (*) có 1 nghiệm.

+ Nếu m + 1 = –1 ⇔ m = –2

⇒ (C ) cắt (d) tại 2 điểm

⇒ phương trình (*) có 2 nghiệm.

+ Nếu –1 < m + 1 < 3 ⇔ –2 < m < 2

⇒ (C ) cắt (d) tại 3 điểm.

⇒ phương trình (*) có 3 nghiệm.

+ Nếu m + 1 = 3 ⇔ m = 2

⇒ (C ) cắt (d) tại 2 điểm.

⇒ phương trình (*) có hai nghiệm.

+ Nếu m + 1 > 3 ⇔ m > 2

⇒ (C ) cắt (d) tại 1 điểm

⇒ phương trình (*) có một nghiệm.

Kết luận : + Với m < -2 hoặc m > 2 thì phương trình có 1 nghiệm.

+ Với m = -2 hoặc m = 2 thì phương trình có 2 nghiệm.

+ Với -2 < m < 2 thì phương trình có 3 nghiệm.

Kiến thức áp dụng