Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thỏa mãn BM = 1/3 BC, CN = 5/4 CA

Giải sách bài tập Toán 10 Bài 6: Tích vô hướng của hai vectơ

Bài 61 trang 105 SBT Toán 10 Tập 1: Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thỏa mãn $BM=\frac{1}{3}BC$ , $CN=\frac{5}{4}CA$ . Tính:

a) $\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{AM}.\overrightarrow{BN}$ .

b) MN.

Lời giải:

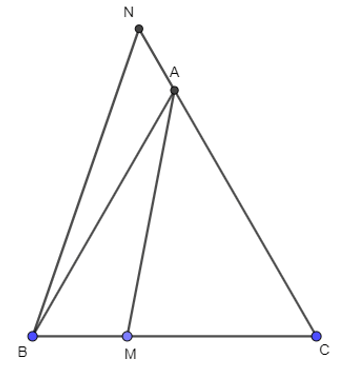
a) Ta có: $\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)$

= $AB.AC.\cos \widehat{BAC}$

= $a.a.\cos 60°$

= $\frac{1}{2}{a}^2$

$\overrightarrow{AM}.\overrightarrow{BN}=\left(\overrightarrow{AB}+\overrightarrow{BM}\right).\left(\overrightarrow{BA}+\overrightarrow{AN}\right)$

$=\left(\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}\right).\left(\frac{1}{4}\overrightarrow{CA}-\overrightarrow{AB}\right)$

$=\left(\overrightarrow{AB}+\frac{1}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\right).\left(-\frac{1}{4}\overrightarrow{AC}-\overrightarrow{AB}\right)$

$=\left(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right).\left(-\frac{1}{4}\overrightarrow{AC}-\overrightarrow{AB}\right)$

$=-\frac{2}{3}\overrightarrow{AB}.\frac{1}{4}\overrightarrow{AC}-\frac{2}{3}\overrightarrow{AB}.\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}.\frac{1}{4}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{AC}.\overrightarrow{AB}$$=-\frac{1}{6}\overrightarrow{AB}.\overrightarrow{AC}-\frac{2}{3}{\overrightarrow{AB}}^2-\frac{1}{12}{\overrightarrow{AC}}^2-\frac{1}{3}\overrightarrow{AC}.\overrightarrow{AB}$

$=-\frac{1}{6}.\frac{1}{2}{a}^2-\frac{2}{3}.a^2-\frac{1}{12}.a^2-\frac{1}{3}.\frac{1}{2}{a}^2$

$=-\frac{1}{12}{a}^2-\frac{2}{3}.a^2-\frac{1}{12}.a^2-\frac{1}{6}{a}^2$

$=-a^2$.

b) Ta có: $\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}$

⇔ $\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}=-\frac{1}{3}\overrightarrow{BC}+\overrightarrow{BC}+\frac{5}{4}\overrightarrow{CA}=\frac{2}{3}\overrightarrow{BC}+\frac{5}{4}\overrightarrow{CA}$

⇔ ${\overrightarrow{MN}}^2={\left(\frac{2}{3}\overrightarrow{BC}+\frac{5}{4}\overrightarrow{CA}\right)}^2$

⇔ ${\overrightarrow{MN}}^2={\left(\frac{2}{3}\overrightarrow{BC}\right)}^2+\frac{5}{3}\overrightarrow{BC}.\overrightarrow{CA}+{\left(\frac{5}{4}\overrightarrow{CA}\right)}^2$

⇔ ${\overrightarrow{MN}}^2={\left(\frac{2}{3}\overrightarrow{BC}\right)}^2-\frac{5}{3}\overrightarrow{CB}.\overrightarrow{CA}+{\left(\frac{5}{4}\overrightarrow{CA}\right)}^2$

⇔ ${\overrightarrow{MN}}^2=\frac{4}{9}{\overrightarrow{BC}}^2-\frac{5}{3}|\overrightarrow{BC}|.|\overrightarrow{CA}|\text{cos}\left(\overrightarrow{CB},\overrightarrow{CA}\right)+\frac{25}{16}{\overrightarrow{CA}}^2$

⇔ ${\overrightarrow{MN}}^2=\frac{4}{9}{\overrightarrow{BC}}^2-\frac{5}{3}|\overrightarrow{BC}|.|\overrightarrow{CA}|\text{cos}\widehat{CBA}+\frac{25}{16}{\overrightarrow{CA}}^2$

⇔ ${\overrightarrow{MN}}^2=\frac{4}{9}{a}^2-\frac{5}{3}a.a\text{cos60}°+\frac{25}{16}{a}^2$

⇔ ${\overrightarrow{MN}}^2=\frac{4}{9}{a}^2-\frac{5}{6}{a}^2+\frac{25}{16}{a}^2=\frac{169}{144}{a}^2$

⇔ $MN=\frac{13}{12}a$

Vậy $MN=\frac{13}{12}a$ .