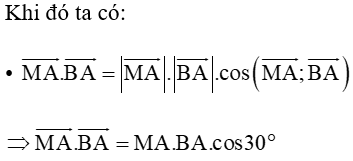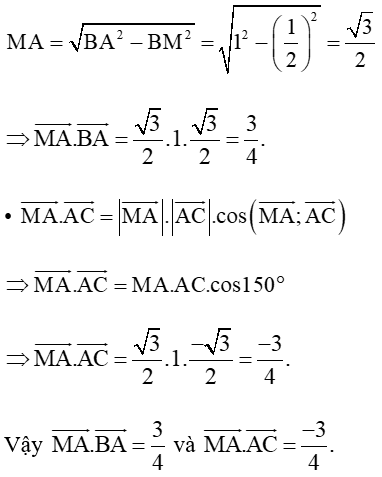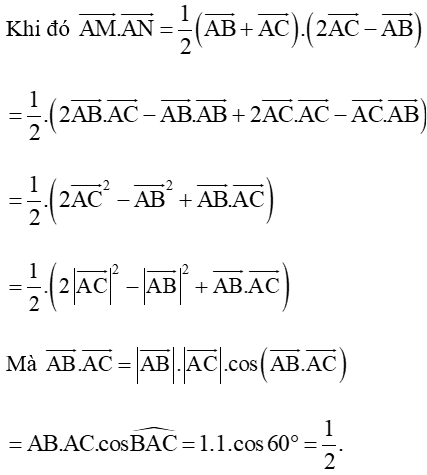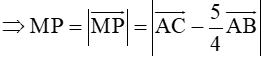Cho tam giác đều ABC có độ dài các cạnh bằng 1
Cho tam giác đều ABC có độ dài các cạnh bằng 1.
Sách bài tập Toán 10 Kết nối tri thức Bài 11: Tích vô hướng của hai vectơ
Bài 4.29 trang 65 sách bài tập Toán lớp 10 Tập 1: Cho tam giác đều ABC có độ dài các cạnh bằng 1.
a) Gọi M là trung điểm của BC. Tính tích vô hướng của các cặp vectơ →MA và →BA, →MA và
b) Gọi N là điểm đối xứng với B qua C. Tính tích vô hướng →AM.→AN.
c) Lấy điểm P thuộc đoạn AN sao cho AP = 3PN. Hãy biểu thị các vectơ →AP,→MP theo hai vectơ →AB và →AC. Tính độ dài đoạn MP.
Lời giải:
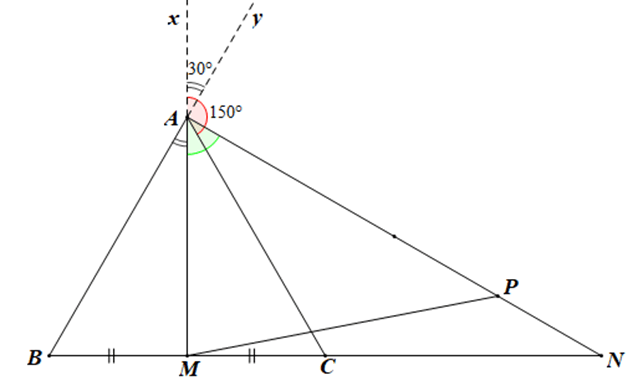
a) Tam giác ABC đều có M là trung điểm của BC nên đường trung tuyến AM đồng thời là đường phân giác và đường cao.
⇒^BAM=^MAC=12^BAC=12.60°=30°
Gọi Ax là tia đối của tia AM, tia Ay là tia đối của tia AB.
Do đó (→MA;→BA)=^xAy=^BAM=30°
(→MA;→AC)=^xAC=180°−^MAC
⇒(→MA;→AC)=180°−30°=150°
Xét tam giác BAM vuông tại M, theo định lí Pythagoras ta có:
b) • Vì M là trung điểm của BC nên →AB+→AC=2→AM
⇒→AM=12(→AB+→AC)
• N đối xứng với B qua C nên C là trung điểm của BN
⇒→AB+→AN=2→AC⇒→AN=2→AC−→AB
Do đó →AM.→AN=12.(2AC2−AB2+→AB.→AC)
=12.(2.12−12+12)
=12.32=34.
Vậy →AM.→AN=34
c) • Vì P thuộc đoạn thẳng AN thỏa mãn AP = 3PN ⇒AP=34AN
⇒→AP=34→AN=34.(2→AC−→AB)
⇒→AP=32→AC−34→AB
• Ta có: →MP=→AP−→AM
=(32→AC−34→AB)−12(→AB+→AC)
=32→AC−34→AB−12→AB−12→AC
=(32→AC−12→AC)−(34→AB+12→AB)
=→AC−54→AB
⇒MP2=(→AC−54→AB)2
=→AC2−2.54→AC.→AB+2516→AB2
=AC2+2516AB2−52→AC.→AB
=12+2516.12−52.12
=2116
⇒MP=√2116=√214.
Vậy →AP=32→AC−34→AB;→MP=→AC−54→AB và MP=√214.
