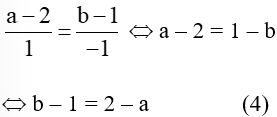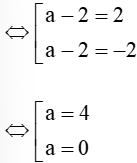Trong mặt phẳng toạ độ Oxy cho hai điểm A(2; 1) và B(4; 3)

Trong mặt phẳng toạ độ Oxy cho hai điểm A(2; 1) và B(4; 3).

Sách bài tập Toán 10 Kết nối tri thức Bài 11: Tích vô hướng của hai vectơ

Bài 4.34 trang 65 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm A(2; 1) và B(4; 3).

a) Tìm toạ độ của điểm C thuộc trục hoành sao cho tam giác ABC vuông tại A. Tính chu vi và diện tích của tam giác ABC.

b) Tìm toạ độ của điểm D sao cho tam giác ABD vuông cân tại A.

Lời giải:

a) Vì tam giác ABC vuông tại A nên AB ⊥ AC hay $\overrightarrow{AB}\perp \overrightarrow{AC}$

Do đó $\overrightarrow{AB}.\overrightarrow{AC}=0$

Giả sử C(x; 0) là điểm thuộc trục hoành.

Với A(2; 1), B(4; 3) và C(x; 0) ta có:

$\overrightarrow{AB}=\left(2;2\right)$ và $\overrightarrow{AC}=\left(x-2;-1\right)$

Khi đó $\overrightarrow{AB}.\overrightarrow{AC}=0$ $\iff$ 2(x – 2) + 2(–1) = 0

$\iff$ 2x – 4 – 2 = 0

$\iff$ 2x = 6

$\iff$ x = 3

Vậy C(3; 0).

$\Rightarrow \overrightarrow{AC}=\left(1;-1\right)$

Ta có:

• $\overrightarrow{AB}=\left(2;2\right)\Rightarrow AB=\sqrt{2^2+2^2}=2\sqrt{2}$

• $\overrightarrow{AC}=\left(1;-1\right)\Rightarrow AC=\sqrt{1^2+{\left(-1\right)}^2}=\sqrt{2}$

• $BC=\sqrt{A{B}^2+A{C}^2}=\sqrt{{\left(2\sqrt{2}\right)}^2+{\left(\sqrt{2}\right)}^2}=\sqrt{10}$ (theo định lí Pythagore)

Khi đó chu vi tam giác ABC là:

AB + AC + BC = $2\sqrt{2}+\sqrt{2}+\sqrt{10}=3\sqrt{2}+\sqrt{10}$ (đơn vị độ dài)

Diện tích tam giác ABC là:

$\frac{1}{2}.AB.AC=\frac{1}{2}.2\sqrt{2}.\sqrt{2}=2$ (đơn vị diện tích)

b) Tam giác ABD vuông cân tại A nên AB ⊥ AD và AB = AD

• Với AB ⊥ AD ta có $\overrightarrow{AB}\perp \overrightarrow{AD}$

Mà $\overrightarrow{AB}\perp \overrightarrow{AC}$ (theo câu a)

Nên $\overrightarrow{AD}$ cùng phương với $\overrightarrow{AC}$

Gọi D(a; b) là tọa độ điểm D cần tìm.

$\Rightarrow \overrightarrow{AD}=\left(a-2;b-1\right)$

Mà $\overrightarrow{AC}=\left(1;-1\right)$

Do đó $\overrightarrow{AD}$ cùng phương với $\overrightarrow{AC}$ khi và chỉ khi:

• Với AB = AD ta có AB² = AD²

$\iff {\left(2\sqrt{2}\right)}^2={\left(a-2\right)}^2+{\left(b-1\right)}^2$

$\iff$ 8 = (a – 2)² + (2 – a)² (do b – 1 = 2 – a)

$\iff$ 8 = 2.(a – 2)²

$\iff$ (a – 2)² = 4

Với a = 4 thì b – 1 = 2 – 4 $\Rightarrow$ b = –1 ta có điểm D₁(4; –1).

Với a = 0 thì b – 1 = 2 – 0 $\Rightarrow$ b = 3 ta có điểm D₂(0; 3).

Vậy có hai điểm D thỏa mãn yêu cầu đề bài là D₁(4; –1) và D₂(0; 3).