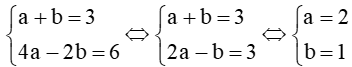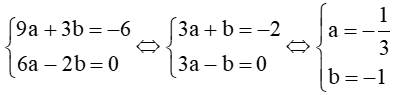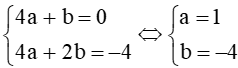Tìm parabol y = ax^2 + bx + 2, biết rằng parabol đó đi qua hai điểm M(1; 5) và N(–2; 8)

Tìm parabol y = ax + bx + 2, biết rằng parabol đó

Sách bài tập Toán 10 Kết nối tri thức Bài 16: Hàm số bậc hai

Bài 6.14 trang 14 Sách bài tập Toán lớp 10 Tập 2: Tìm parabol y = ax² + bx + 2, biết rằng parabol đó

a) đi qua hai điểm M(1; 5) và N(–2; 8);

b) đi qua điểm A(3; –4) và có trục đối xứng $x=-\frac{3}{2}$;

c) có đỉnh I(2; –2).

Lời giải:

a)

Do parabol y = ax² + bx + 2 đi qua M(1; 5) nên ta có:

a.1² + b.1 + 2 = 5 ⇔ a + b = 3 (1)

Do parabol y = ax² + bx + 2 đi qua N(–2; 8) nên ta có:

a.(–2)² + b.(–2) + 2 = 8 ⇔ 4a – 2b = 6 (2)

Từ (1) và (2) ta có:

Vậy parabol cần tìm là: y = 2x² + x + 2.

b)

Do parabol y = ax² + bx + 2 đi qua A(3; –4) nên ta có:

a.3² + b.3 + 2 = –4 ⇔ 9a + 3b = –6 (3)

Do parabol y = ax² + bx + 2 có trục đối xứng $x=-\frac{3}{2}$ nên ta có:

$\frac{-b}{2a}=-\frac{3}{2}$ ⇔ –2b = –6a ⇔ 6a – 2b = 0 (4)

Từ (3) và (4) ta có:

Vậy parabol cần tìm là: y = $-\frac{1}{3}{x}^2-x+2$.

c)

Do parabol y = ax² + bx + 2 có đỉnh I(2; –2) nên ta có:

$\frac{-b}{2a}=2$ ⇔ –b = 4a ⇔ 4a + b = 0 (5)

Và a.2² + b.2 + 2 = –2 ⇔ 4a + 2b = –4 (6)

Từ (5) và (6) ta có:

Vậy parabol cần tìm là: y = x² – 4x + 2.