Xác định dấu của các hệ số a, b, c và dấu của biệt thức ∆ = b^2 – 4ac

Xác định dấu của các hệ số a, b, c và dấu của biệt thức ∆ = b – 4ac của hàm số bậc hai y = ax + bx + c, biết đồ thị của nó có dạng như Hình 6.16.

Sách bài tập Toán 10 Kết nối tri thức Bài 16: Hàm số bậc hai

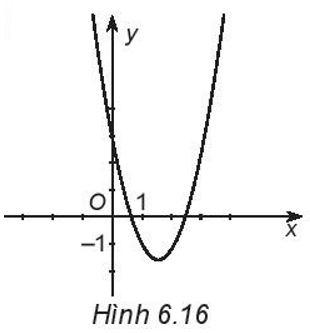
Bài 6.16 trang 14 Sách bài tập Toán lớp 10 Tập 2: Xác định dấu của các hệ số a, b, c và dấu của biệt thức ∆ = b² – 4ac của hàm số bậc hai y = ax² + bx + c, biết đồ thị của nó có dạng như Hình 6.16.

Lời giải:

Từ đồ thị của hàm số ta thấy:

+ Đồ thị quay bề lõm quay lên trên nên a > 0.

+ Đồ thị cắt trục tung tại điểm có tung độ dương nên ta có: a.0² + b.0 + c > 0 ⇔ c > 0.

+ Hoành độ đỉnh $x=-\frac{b}{2a}$ có giá trị dương nên a và b trái dấu. Vì a > 0 nên b < 0.

+ Mặt khác, vì đồ thị hàm số cắt trục hoành Ox tại hai điểm phân biệt, tức là phương trình ax² + bx + c = 0 có hai nghiệm phân biệt nên ∆ = b² – 4ac > 0.

Vậy a > 0, b < 0, c > 0 và ∆ = b² – 4ac > 0.