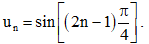Xét tính tăng, giảm của mỗi dãy số (un), biết

❮ Bài trước Bài sau ❯

Giải sách bài tập Toán 11 Bài 1: Dãy số

Bài 11 trang 46 SBT Toán 11 Tập 1: Xét tính tăng, giảm của mỗi dãy số (u_n), biết:

a) u_n = 2n + 3;

b) u_n = 3ⁿ – n;

c) $u_{n} = \frac{\sqrt{n}}{2^{n}}$ ;

d) u_n = sin n.

Lời giải:

a) Ta có u_{n + 1} = 2(n + 1) + 3 = 2n + 5.

Xét u_{n + 1} – u_n = (2n + 5) – (2n + 3) = 2 > 0 với mọi n ∈ ℕ^*.

Do đó, u_{n + 1} > u_n với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với u_n = 2n + 3 là dãy số tăng.

b) Ta có u_{n + 1} = 3^{n + 1} – (n + 1) = 3 . 3ⁿ – n – 1.

Xét u_{n + 1} – u_n = (3 . 3ⁿ – n – 1) – (3ⁿ – n) = 3 . 3ⁿ – 3ⁿ – 1 = 2 . 3ⁿ – 1 > 0 với mọi n ∈ ℕ^*.

Do đó, u_{n + 1} > u_n với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với u_n = 3ⁿ – n là dãy số tăng.

c) Ta có u_{n + 1} = $\frac{\sqrt{n + 1}}{2^{n + 1}}$ = $\frac{\sqrt{n + 1}}{{2.2}^{n}}$ .

Xét $u_{n + 1} - u_{n} = \frac{\sqrt{n + 1}}{{2.2}^{n}} - \frac{\sqrt{n}}{2^{n}} = \frac{\sqrt{n + 1} - 2 \sqrt{n}}{{2.2}^{n}}$ $= \frac{\sqrt{n + 1} - \sqrt{4 n}}{{2.2}^{n}}$

$= \frac{n + 1 - 4 n}{{2.2}^{n} (\sqrt{n + 1} + \sqrt{4 n})} = \frac{- 3 n + 1}{{2.2}^{n} (\sqrt{n + 1} + \sqrt{4 n})} < 0$ với mọi n ∈ ℕ^*.

(do – 3n + 1 < 0, 2ⁿ > 0 và với mọi n ∈ ℕ^*).

Do vậy, u_{n + 1} < u_n với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với $u_{n} = \frac{\sqrt{n}}{2^{n}}$ là dãy số giảm.

Lời giải Sách bài tập Toán lớp 11 Bài 1: Dãy số Cánh diều hay khác:

Bài 14 trang 46 SBT Toán 11 Tập 1: Với mỗi số nguyên dương n, lấy n + 6 điểm cách đều nhau trên đường tròn. Nối mỗi điểm ....

Xem thêm lời giải Sách bài tập Toán 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯