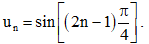Bài 13 trang 46 SBT Toán 11 Tập 1

Chứng minh rằng:

Giải sách bài tập Toán 11 Bài 12 trang 46 SBT Toán 11 Tập 1

Bài 13 trang 46 SBT Toán 11 Tập 1: Chứng minh rằng:

a) Dãy số (u_n) với $u_{n} = \sqrt{n^{2} + 1}$ bị chặn dưới;

b) Dãy số (u_n) với u_n = – n²– n bị chặn trên;

c) Dãy số (u_n) với $u_{n} = \frac{2 n + 1}{n + 2}$ bị chặn.

Lời giải:

a) Ta có n² ≥ 1 với mọi n ∈ ℕ^*.

Do đó, $\sqrt{n^{2} + 1} \geq \sqrt{1 + 1} = \sqrt{2}$ với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với $u_{n} = \sqrt{n^{2} + 1}$ bị chặn dưới.

b) Ta có – n² – n ≤ – 2 với mọi n ∈ ℕ^*.

Do đó, dãy số (u_n) với u_n = – n²– n bị chặn trên.

c) Ta có $\frac{2 n + 1}{n + 2} > 0$ với mọi n ∈ ℕ^*. Do đó, dãy số (u_n) với $u_{n} = \frac{2 n + 1}{n + 2}$ bị chặn dưới. (1)

Lại có $\frac{2 n + 1}{n + 2} = \frac{2 (n + 2) - 3}{n + 2} = 2 - \frac{3}{n + 2} < 2$ với mọi n ∈ ℕ^*.

Do đó, dãy số (u_n) với $u_{n} = \frac{2 n + 1}{n + 2}$ bị chặn trên. (2)

Từ (1) và (2), suy ra dãy số (u_n) với $u_{n} = \frac{2 n + 1}{n + 2}$ bị chặn.

Lời giải Sách bài tập Toán lớp 11 Bài 12 trang 46 SBT Toán 11 Tập 1 Cánh diều hay khác:

Bài 14 trang 46 SBT Toán 11 Tập 1: Với mỗi số nguyên dương n, lấy n + 6 điểm cách đều nhau trên đường tròn. Nối mỗi điểm ....