Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được
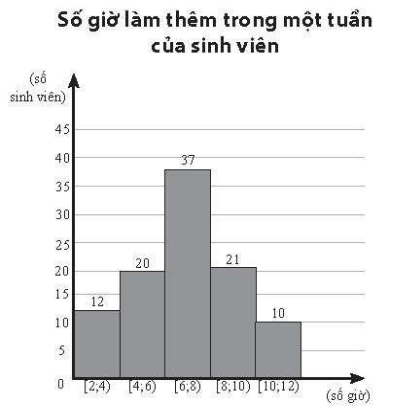
Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên.
Giải sách bài tập Toán 11 Bài tập cuối chương 5 - Chân trời sáng tạo
Bài 5 trang 162 SBT Toán 11 Tập 1: Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên.
Hãy ước lượng số trung bình, mốt và các tứ phân vị của số liệu đó.
Lời giải:
Từ mẫu số liệu ghép nhóm, ta có bảng thống kê số giờ làm thêm trong một tuần của 100 sinh viên như sau:
|
Số giờ làm thêm |
[2; 4) |
[4; 6) |
[6; 8) |
[8; 10) |
[10; 12) |
|
Số giờ làm thêm đại diện |
3 |
5 |
7 |
9 |
11 |
|
Số sinh viên |
12 |
20 |
37 |
21 |
10 |
Cỡ mẫu n = 100.
Số trung bình của mẫu số liệu ghép nhóm trên là
ˉx=3⋅12+5⋅20+7⋅37+9⋅21+11⋅10100 = 6,94.
Nhóm chứa mốt của mẫu số liệu trên là nhóm [6; 8).
Do đó: um = 6; nm = 37; nm ‒ 1 = 20; nm + 1 = 21; um + 1 =8.
Vậy mốt của mẫu số liệu ghép nhóm là
MO=6+37−20(37−20)+(37−21)⋅(8−6)=23233≈7,03.
Gọi x1; x2; ...; x100 là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ hai của mẫu số liệu x1; x2; ...; x100 là 12(x50+x51). Do x50 và x51 thuộc nhóm [6; 8) nên tứ phân vị thứ hai của mẫu số liệu là
Q2=6+1002−(12+20)37⋅(8−6)=25837≈6,97.
Tứ phân vị thứ nhất của dãy số liệu x1; x2; ...; x100 là 12(x25+x26). Do x25 và x26 thuộc nhóm [4; 6) nên tứ phân vị thứ nhất của mẫu số liệu là
Q1=4+1004−(12+0)20⋅(6−4) = 5,3.
Tứ phân vị thứ ba của dãy số liệu x1; x2; ...; x100 là 12(x75+x76). Do x75 và x76 thuộc nhóm [8; 10) nên tứ phân vị thứ ba của mẫu số liệu là
Q3=8+3⋅1004−(12+20+37)21⋅(10−8)=607≈8,57.
Lời giải SBT Toán 11 Bài tập cuối chương 5 hay khác:
Câu 1 trang 160 SBT Toán 11 Tập 1: Tổng số học sinh tham gia kì thi đánh giá năng lực trên là ....
Câu 6 trang 160 SBT Toán 11 Tập 1: 160,5 là giá trị đại diện cho nhóm ....