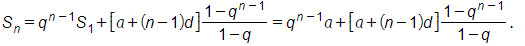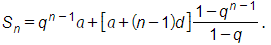Một dãy số un được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi

Một dãy số (u) được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi

Giải sách bài tập Toán 11 Bài tập cuối chương 2 - Kết nối tri thức

Bài 2.50 trang 43 SBT Toán 11 Tập 1: Một dãy số (u_n) được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi

u₁ = a, u_{n + 1} = qu_n + d.

Nếu q = 1 ta có cấp số cộng với công sai d, còn nếu d = 0 ta có cấp số nhân với công bội q.

a) Giả sử q ≠ 1. Dự đoán công thức số hạng tổng quát u_n.

b) Thiết lập công thức tính tổng S_n của n số hạng đầu của cấp số nhân cộng (u_n).

Lời giải:

a) Ta viết lần lượt các số hạng của dãy:

u₁ = a;

u₂ = qu₁ + d;

u₃ = qu₂ + d = q(qu₁ + d) + d = q²u₁ + qd + d = q²u₁+ d(q + 1);

u₄ = qu₃+ d = q(q²u₁ + qd + d) + d = q³u₁ + q²d + qd + d

= q³u₁ + d(q² + q + 1) = q³u₁ + d $\frac{1 - q^{3}}{1 - q}$ (với q ≠ 1).

Làm tương tự ta được công thức số hạng tổng quát u_n:

u_n = q^{n – 1}u₁ + d(q^{n – 2} + q^{n – 3} + ... + 1) = q^{n – 1}u₁ + d $\frac{1 - q^{n - 1}}{1 - q}$ .

b) Ta viết tổng n số hạng đầu như sau

S_n = u₁ + u₂ + ... + u_n

= u₁ + (qu₁ + d) + (qu₂ + d) + ... + (qu_{n – 1} + d)

= u₁ + q(u₁ + u₂ + ... + u_{n – 1}) + (n – 1)d

= u₁ + qS_{n – 1}+ (n – 1)d

= qS_{n – 1} + a + (n – 1)d (vì u₁ = a).

Như vậy, ta được (S_n) cũng là một cấp số nhân cộng với S₁ = u₁ = a.

Áp dụng công thức số hạng tổng quát vừa tìm được ở câu a để tính S_n ta có

Một dãy số un được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi

Vậy Một dãy số un được gọi là một cấp số nhân cộng nếu nó cho bởi hệ thức truy hồi

Lời giải SBT Toán 11 Bài tập cuối chương 2 hay khác: