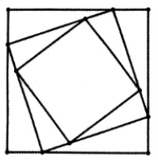
Cho hình vuông H1 có cạnh bằng a. Chia mỗi cạnh của hình vuông này thành bốn phần bằng nhau

Cho hình vuông H có cạnh bằng a. Chia mỗi cạnh của hình vuông này thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông H. Lặp lại cách làm như trên với hình vuông H để được hình vuông H. Tiếp tục quá trình trên ta nhận được dãy hình vuông H, H, H, ..., H, ... Gọi s là diện tích của hình vuông H.

Giải sách bài tập Toán 11 Bài tập cuối Chương 5 - Kết nối tri thức

Bài 5.44 trang 89 SBT Toán 11 Tập 1: Cho hình vuông H₁ có cạnh bằng a. Chia mỗi cạnh của hình vuông này thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông H₂. Lặp lại cách làm như trên với hình vuông H₂ để được hình vuông H₃. Tiếp tục quá trình trên ta nhận được dãy hình vuông H₁, H₂, H₃, ..., H_n, ... Gọi s_n là diện tích của hình vuông H_n.

a) Tính s_n.

b) Tính tổng T = s₁ + s₂ + ... + s_n + ...

Lời giải:

a) Áp dụng định lí Pythagore, ta có cạnh của hình vuông H₂ là

$a_2=\sqrt{{\left(\frac{a}{4}\right)}^2+{\left(\frac{3a}{4}\right)}^2}=a\sqrt{\frac{5}{8}}$.

Khi đó diện tích của hình vuông H₂ là $s_2={\left(a\sqrt{\frac{5}{8}}\right)}^2=\frac{5}{8}{a}^2$ .

Mà diện tích của hình vuông H₁ là s₁ = a².

Do đó, $s_2=\frac{5}{8}{a}^2=\frac{5}{8}{s}_1$ .

Lí luận tương tự, ta có $s_3=\frac{5}{8}{s}_2,\mathrm{....,}{s}_n=\frac{5}{8}{s}_{n-1}={\left(\frac{5}{8}\right)}^{n-1}{a}^2$ .

b) Ta có T = s₁ + s₂ + ... + s_n + ... $=a^2\left(1+\frac{5}{8}+{\left(\frac{5}{8}\right)}^2+\mathrm{...}+{\left(\frac{5}{8}\right)}^{n-1}+\mathrm{...}\right)$ .

Vì $\mathrm{1,}\frac{5}{8},{\left(\frac{5}{8}\right)}^2\mathrm{,...,}{\left(\frac{5}{8}\right)}^{n-1}\mathrm{,...}$ là cấp số nhân lùi vô hạn với u₁ = 1 và công bội q = $\frac{5}{8}$ nên

$1+\frac{5}{8}+{\left(\frac{5}{8}\right)}^2+\mathrm{...}+{\left(\frac{5}{8}\right)}^{n-1}+\mathrm{...}=\frac{1}{1-\frac{5}{8}}=\frac{8}{3}$.

Vậy $T=\frac{8a^2}{3}$ .

Lời giải SBT Toán 11 Bài tập cuối Chương 5 hay khác:

• Bài 5.26 trang 87 SBT Toán 11 Tập 1: Cho hai dãy số (u_n) và (v_n) thỏa mãn $\underset{n\to +\infty }{\lim }{u}_n=1$ và $\underset{n\to +\infty }{\lim }{v}_n=b\in ℝ$. Xét các khẳng định sau ....

• Bài 5.27 trang 87 SBT Toán 11 Tập 1: Cho $L=\underset{n\to +\infty }{\lim }\left(n^3-2n+1\right)$ . Giá trị của L là ....

• Bài 5.28 trang 87 SBT Toán 11 Tập 1: Biết $\underset{n\to +\infty }{\lim }\frac{2n^2+n-1}{a{n}^2+1}=1$ với a là tham số. Giá trị của a² – 2a là ....

• Bài 5.29 trang 87 SBT Toán 11 Tập 1: Cho $u_n=\sqrt{n}\left(\sqrt{n+2}-\sqrt{n+1}\right)$. Khi đó $\underset{n\to +\infty }{\lim }{u}_n$ bằng ....

• Bài 5.30 trang 87 SBT Toán 11 Tập 1: Tính tổng $S=-\frac{2}{3}+\frac{2}{9}-\frac{2}{27}+\mathrm{...}+{\left(-1\right)}^n\frac{2}{3^n}+\mathrm{...}$ ....

• Bài 5.31 trang 87 SBT Toán 11 Tập 1: Cho hàm số f(x) thỏa mãn $\underset{x\to 1^{+}}{\lim }f\left(x\right)=3$ và $\underset{x\to 1^{-}}{\lim }f\left(x\right)=-3$. Khẳng định đúng là ....

• Bài 5.32 trang 88 SBT Toán 11 Tập 1: Cho hàm số f(x) thỏa mãn $\underset{x\to 1^{+}}{\lim }f\left(x\right)=2$ và $\underset{x\to 1^{-}}{\lim }f\left(x\right)=m+1$ ....

• Bài 5.33 trang 88 SBT Toán 11 Tập 1: Biết hàm số $f\left(x\right)=\left\{\begin{array}{l}{x}^2+an{ê}^{\text{'}}ux\le 1\\ 2x+bn{ê}^{\text{'}}ux>1\end{array}\right.$ có giới hạn khi x → 1. Giá trị của a – b bằng ....

• Bài 5.34 trang 88 SBT Toán 11 Tập 1: Giới hạn $\underset{x\to 1^{+}}{\lim }\frac{x-1}{\sqrt{x-1}}$ là ....

• Bài 5.35 trang 88 SBT Toán 11 Tập 1: Cho $f\left(x\right)=\frac{x^2-x}{\left|x\right|}$. Khi đó, giới hạn $\underset{x\to 0}{\lim }f\left(x\right)$ là ....

• Bài 5.36 trang 88 SBT Toán 11 Tập 1: Giới hạn $\underset{x\to -\infty }{\lim }\frac{\sqrt{x^2+2}-x}{x}$ là ....

• Bài 5.37 trang 88 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}2n{ê}^{\text{'}}u-1<x\le 1\\ 1-xn{ê}^{\text{'}}ux\le -1hoacx>1\end{array}\right.$. Mệnh đề đúng là ....

• Bài 5.38 trang 88 SBT Toán 11 Tập 1: Xét hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2+3x+2}{x+1}n{ê}^{\text{'}}ux\ne -1\\ mn{ê}^{\text{'}}ux=-1\end{array}\right.$ với m là tham số. Hàm số f(x) liên tục trên ℝ khi ....

• Bài 5.39 trang 89 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{x\left(x-1\right)}{\sqrt{x-1}}$. Hàm số này liên tục trên ....

• Bài 5.40 trang 89 SBT Toán 11 Tập 1: Cho phương trình x⁷ + x⁵ = 1. Mệnh đề đúng là ....

• Bài 5.41 trang 89 SBT Toán 11 Tập 1: Cho dãy số (u_n) thỏa mãn |u_n| ≤ 1. Tính $\underset{n\to +\infty }{\lim }\frac{u_n}{n+1}$. ....

• Bài 5.42 trang 89 SBT Toán 11 Tập 1: Tìm giới hạn của dãy số (u_n) với $u_n=\frac{n\sqrt{1+2+\mathrm{...}+n}}{2n^2+3}$. ....

• Bài 5.43 trang 89 SBT Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số ....

• Bài 5.45 trang 89 SBT Toán 11 Tập 1: Tìm a là số thực thỏa mãn $\underset{x\to +\infty }{\lim }\left(\frac{2x^2+1}{x^2+2x+3}+a^2+3a\right)=0$. ....

• Bài 5.46 trang 89 SBT Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 5.47 trang 90 SBT Toán 11 Tập 1: Tính $\underset{x\to -\infty }{\lim }\left(1-x\right)\left(1-2x\right)\mathrm{...}\left(1-2018x\right)$. ....

• Bài 5.48 trang 90 SBT Toán 11 Tập 1: Biết $\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$. Hãy tính: ....

• Bài 5.49 trang 90 SBT Toán 11 Tập 1: Tính $\underset{x\to 0}{\lim }x\sin \frac{1}{x}$. ....

• Bài 5.50 trang 90 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{\sqrt{x-1}-\sqrt{1-x}}{x}$. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu để hàm số f(x) liên tục tại x = 0? ....

• Bài 5.51 trang 90 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{1}{x}n{ê}^{\text{'}}ux\ne 0\\ 2n{ê}^{\text{'}}ux=0\end{array}\right.$. ....

• Bài 5.52 trang 90 SBT Toán 11 Tập 1: Một điểm dịch vụ trông giữ xe ô tô thu phí 30 nghìn đồng trong giờ đầu tiên và thu thêm ....