Bạn Minh có 2 hộp đựng thẻ. Hộp thứ nhất có 4 thẻ vàng và 1 thẻ đỏ. Hộp thứ hai có 6 thẻ vàng và 2 thẻ đỏ
Bạn Minh có 2 hộp đựng thẻ. Hộp thứ nhất có 4 thẻ vàng và 1 thẻ đỏ. Hộp thứ hai có 6 thẻ vàng và 2 thẻ đỏ. Các thẻ có cùng kích thước. Minh chọn ngẫu nhiên từ hộp thứ nhất 2 thẻ và bỏ vào hộp thứ hai. Sau đó, minh lại chọn ngẫu nhiên từ hộp thứ hai ra 2 thẻ.
Giải SBT Toán 12 Chân trời sáng tạo Bài 2: Công thức xác suất toàn phần và công thức Bayes
Bài 2 trang 84 SBT Toán 12 Tập 2: Bạn Minh có 2 hộp đựng thẻ. Hộp thứ nhất có 4 thẻ vàng và 1 thẻ đỏ. Hộp thứ hai có 6 thẻ vàng và 2 thẻ đỏ. Các thẻ có cùng kích thước. Minh chọn ngẫu nhiên từ hộp thứ nhất 2 thẻ và bỏ vào hộp thứ hai. Sau đó, minh lại chọn ngẫu nhiên từ hộp thứ hai ra 2 thẻ.
a) Tính xác suất để 2 thẻ được chọn ra từ hộp thứ hai đều có màu đỏ.
b) Biết rằng 2 thẻ được chọn ra từ hộp thứ hai đều có màu đỏ, tính xác suất của biến cố 2 thẻ lấy ra từ hộp thứ nhất có cùng màu.
Lời giải:
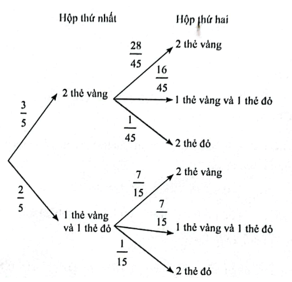
a) Ta có sơ đồ hình cây như sau:
Gọi A là biến cố “2 thẻ được chọn từ hộp thứ hai đều có màu đỏ” và B là biến cố “2 thẻ lấy ra từ hộp thứ nhất có cùng màu”.
Như vậy, từ sơ đồ hình cây, ta có xác suất 2 thẻ được chọn ra từ hộp thứ hai đều có màu đỏ là P(A) =
b) Xác suất để 2 thẻ lấy ra từ hộp thứ nhất có cùng màu là P(B) = = 0,6.
Xác suất để 2 thẻ được chọn từ hộp thứ hai đều có màu đỏ, biết rằng 2 thẻ lấy ra từ hộp thứ nhất có cùng màu là P(A | B) =
Theo công thức Bayes, xác suất của biến cố 2 thẻ lấy ra từ hộp thứ nhất có cùng màu, biết rằng 2 thẻ được chọn ra từ hộp thứ hai đều có màu đỏ là:
≈ 0,333.
Lời giải SBT Toán 12 Bài 2: Công thức xác suất toàn phần và công thức Bayes hay khác: