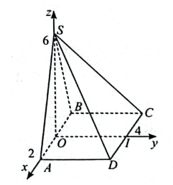
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác cân tại S

❮ Bài trước Bài sau ❯

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác cân tại S có chiều cao bằng 6 và nằm trong mặt phẳng vuông góc với đáy.

Giải SBT Toán 12 Chân trời sáng tạo Bài 2: Phương trình đường thẳng trong không gian

Bài 6 trang 55 SBT Toán 12 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác cân tại S có chiều cao bằng 6 và nằm trong mặt phẳng vuông góc với đáy.

a) Tính góc α giữa hai đường thẳng SD và BC;

b) Tính góc β giữa hai mặt phẳng (SAD) và (SCD).

Lời giải:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác cân tại S

Gọi O là trung điểm của AB, suy ra SO ⊥ (ABCD).

Chọn hệ trục Oxyz như hình bên.

Ta có: S(0; 0; 6), A(2; 0; 0), B(−2; 0; 0), C(−2; 4; 0), D(2; 4; 0).

a) Ta có: $\vec{S D} = (2; 4; - 6), \vec{B C} = (0; 4; 0)$

Suy ra cosα = $\frac{|\vec{S D} . \vec{B C}|}{|\vec{S D}| . |\vec{B C}|} = \frac{|2.0 + 4.4 - 6.0|}{\sqrt{2^{2} + 4^{2} + {(- 6)}^{2}} . \sqrt{0^{2} + 4^{2} + 0^{2}}} = \frac{\sqrt{14}}{7}$ ⇒ α ≈ 57,7°.

b) Mặt phẳng (SAD) có cặp vectơ chỉ phương là $\vec{S D} = (2; 4; - 6)$ , $\vec{S A} = (2; 0; - 6)$

Ta có: $[\vec{S D}, \vec{S A}] = (|\begin{matrix} 4 & - 6 \\ 0 & - 6 \end{matrix}|; |\begin{matrix} - 6 & 2 \\ - 6 & 2 \end{matrix}|; |\begin{matrix} 2 & 4 \\ 2 & 0 \end{matrix}|)$ = (−24; 0; −8) = −8(3; 0; 1).

Vậy $\vec{n} = (3; 0; 1)$ là vectơ pháp tuyến của (SAD).

Mặt phẳng (SCD) có cặp vectơ chỉ phương là: $\vec{D C} = (- 4; 0; 0)$ , $\vec{S D} = (2; 4; - 6)$

Ta có: $[\vec{S D}, \vec{D C}] = (|\begin{matrix} 4 & - 6 \\ 0 & 0 \end{matrix}|; |\begin{matrix} - 6 & 2 \\ 0 & - 4 \end{matrix}|; |\begin{matrix} 2 & 4 \\ - 4 & 0 \end{matrix}|)$ = (0; 24; 16) = 8(0; 3; 2).

Vậy $\vec{n^{'}} = (0; 3; 2)$

Suy ra cosβ = $\frac{\vec{n} . \vec{n^{'}}}{|\vec{n}| . |\vec{n^{'}}|} = \frac{|3.0 + 0.3 + 1.2|}{\sqrt{3^{2} + 0^{2} + 1^{2}} . \sqrt{0^{2} + 3^{2} + 2^{2}}} = \frac{2}{\sqrt{130}}$ ⇒ β ≈ 79,9°.

Lời giải SBT Toán 12 Bài 2: Phương trình đường thẳng trong không gian hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯