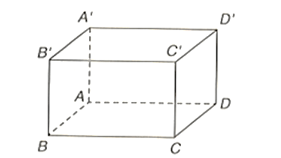
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi x, y, z theo thứ tự là số đo các góc

Cho hình hộp chữ nhật ABCD.A

Giải SBT Toán 12 Chân trời sáng tạo Bài 1: Vectơ và các phép toán trong không gian

Bài 8 trang 64 SBT Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi x, y, z theo thứ tự là số đo các góc hợp bởi vectơ $\vec{A C^{'}}$ với các vectơ $\vec{A B}, \vec{A D}, \vec{A A^{'}}$ .

Chứng minh cos²x + cos²y + cos²_Z = 1.

Lời giải:

Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi x, y, z theo thứ tự là số đo các góc

Gọi a, b, c, d lần lượt là độ dài của AB, AD, AA' và AC'.

Ta có: $A {C^{'}}^{2} = A B^{2} + A D^{2} + A {A^{'}}^{2}$

⇔ d² = a² + b² + c², cosx = $\frac{a}{d}$ , cosy = $\frac{b}{d}$ , cosz = $\frac{c}{d}$ .

Suy ra cos²x + cos²y + cos²z = ${(\frac{a}{d})}^{2} + {(\frac{b}{d})}^{2} + {(\frac{c}{d})}^{2}$ = $\frac{a^{2} + b^{2} + c^{2}}{d^{2}} = \frac{d^{2}}{d^{2}} = 1$ .

Vậy cos²x + cos²y + cos²_Z = 1.

Lời giải SBT Toán 12 Bài 1: Vectơ và các phép toán trong không gian hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯