Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau

Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau:

Giải sách bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

Bài 1.3 trang 9 SBT Toán 12 Tập 1: Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau:

a) $y = x + \frac{1}{x}$ ;

b) $y = \frac{x}{x^{2} + 1} .$

Lời giải:

a) $y = x + \frac{1}{x}$

Tập xác định: D = ℝ\{0}.

Ta có: y' = 1 – $\frac{1}{x^{2}}$ = $\frac{x^{2} - 1}{x^{2}}$

y' = 0 ⇔ $\frac{x^{2} - 1}{x^{2}}$ = 0 ⇔ x = ±1.

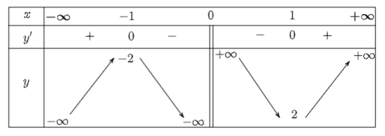
Ta có bảng biến thiên:

Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau

Từ bảng biến thiên, ta có:

Hàm số nghịch biến trên các khoảng (−1; 0) và (0; 1).

Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).

Hàm số đạt cực đại tại x = −1 và y_CĐ = y(−1) = −2.

Hàm số đạt cực tiểu tại x = 1 và y_CT = y(1) = 2.

b) $y = \frac{x}{x^{2} + 1} .$

Tập xác định: D = ℝ.

Ta có: y' = $\frac{1 - x^{2}}{{(x^{2} + 1)}^{2}}$

y' = 0 ⇔ $\frac{1 - x^{2}}{{(x^{2} + 1)}^{2}}$ = 0 ⇔ 1 – x² = 0 ⇔ x = ±1.

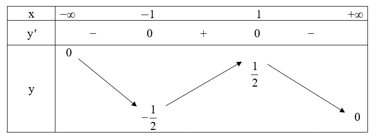
Ta có bảng biến thiên như sau:

Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau

Từ bảng biến thiên, ta có:

Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).

Hàm số đồng biến trên khoảng (−1; 1).

Hàm số đạt cực đại tại x = 1 và y_CĐ = y(1) = $\frac{1}{2}$ .

Hàm số đạt cực tiểu tại x = −1 và y_CT = y(−1) = $\frac{1}{2}$ .

Lời giải Sách bài tập Toán lớp 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay khác: