Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm

Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1 000 và R(x) = 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra.

Giải sách bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

Bài 1.8 trang 9 SBT Toán 12 Tập 1: Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1 000 và R(x) = 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra.

a) Tính hàm lợi nhuận trung bình $\overline{P}\left(x\right)=\frac{R\left(x\right)-C\left(x\right)}{x}$ .

b) Tìm lợi nhuận trung bình khi mức sản xuất x lần lượt là 100, 500 và 1 000 đơn vị sản phẩm.

c) Xét tính đơn điệu của hàm lợi nhuận trung bình $\overline{P}\left(x\right)$  trên khoảng (0; +∞) và tính giới hạn của hàm số này khi x → +∞. Giải thích ý nghĩa thực tiễn của kết quả nhận được.

Lời giải:

a) Ta có:

$\overline{P}\left(x\right)=\frac{R\left(x\right)-C\left(x\right)}{x}=\frac{75,5x-25,5x-1000}{x}=50-\frac{1000}{x}$  (triệu đồng).

Tập xác định của hàm lợi nhuận trung bình là: (0; +∞).

b) Với x = 100 thì $\overline{P}\left(100\right)=50-\frac{1000}{100}=40$  (triệu đồng).

    Với x = 500 thì $\overline{P}\left(500\right)=50-\frac{1000}{500}=48$  (triệu đồng).

    Với x = 1 000 thì $\overline{P}\left(1000\right)=50-\frac{1000}{1000}=49$  (triệu đồng).

c) Ta có: $\overline{P}\left(x\right)=50-\frac{1000}{x}$

           $\overline{P^{\text{'}}}\left(x\right)=\frac{1000}{x^2}$ > 0 với mọi x ∈ (0; +∞).

Vậy hàm lợi nhuận trung bình đồng biến trên khoảng (0; +∞).

Mặt khác, $\underset{x\to +\infty }{\lim }\overline{P}\left(x\right)=\underset{x\to +\infty }{\lim }\left(50-\frac{1000}{x}\right)=50.$

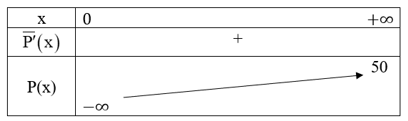
Ta có bảng biến thiên như sau:

Như vậy, mặc dù lợi nhuận trung bình luôn tăng khi mức sản xuất tăng nhưng không vượt quá 50 triệu đồng.

Lời giải Sách bài tập Toán lớp 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay khác:

• Bài 1.1 trang 8 SBT Toán 12 Tập 1: Cho hàm f(x) xác định trên ℝ và đạo hàm f'(x) có đồ thị như hình bên. Sử dụng đồ thị hàm số y = f'(x) ....

• Bài 1.2 trang 9 SBT Toán 12 Tập 1: Tìm các khoảng đồng biến, khoảng nghịch biến và cực trị (nếu có) của các hàm số sau: ....

• Bài 1.3 trang 9 SBT Toán 12 Tập 1: Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau: ....

• Bài 1.4 trang 9 SBT Toán 12 Tập 1: Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau: ....

• Bài 1.5 trang 9 SBT Toán 12 Tập 1: Tìm các giá trị của tham số m sao cho hàm số y = x³ + mx² + 3x + 2 đồng biến trên ℝ ....

• Bài 1.6 trang 9 SBT Toán 12 Tập 1: Chứng minh rằng hàm số $\mathrm{f}\left(\mathrm{x}\right)=\sqrt[3]{{\mathrm{x}}^2}$  không có đạo hàm tại x = 0 nhưng có cực tiểu tại điểm x = 0 ....

• Bài 1.7 trang 9 SBT Toán 12 Tập 1: Một nhà phân phối đồ chơi trẻ em xác định hàm chi phí C(x) và hàm doanh thu R(x) ....

• Bài 1.9 trang 10 SBT Toán 12 Tập 1: Một con lắc lò xo, gồm một vật nặng có khối lượng 1 kg được gắn vào một lò xo được cố định một đầu ....

• Bài 1.10 trang 10 SBT Toán 12 Tập 1: Một vật chuyển động dọc theo trục số nằm ngang, chiều dương từ trái sang phải ....