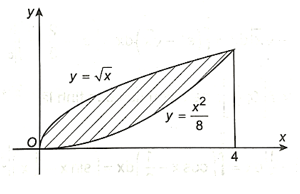
Xét hình phẳng giới hạn bởi các đường y = căn bậc hai x, y = x^2/8, x = 0, x = 4

Giải sách bài tập Toán 12 Bài 13: Ứng dụng hình học của tích phân - Kết nối tri thức

Bài 4.25 trang 17 SBT Toán 12 Tập 2: Xét hình phẳng giới hạn bởi các đường y = $\sqrt{\mathrm{x}}$, y = $\frac{{\mathrm{x}}^2}{8}$, x = 0, x = 4.

a) Tính diện tích hình phẳng.

b) Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng xung quanh trục Ox.

Lời giải:

a) Ta có đồ thị hàm số như sau:

Quan sát đồ thị, ta thấy đồ thị hàm số y = $\sqrt{\mathrm{x}}$ nằm phía trên đồ thị hàm số y = $\frac{{\mathrm{x}}^2}{8}$ so với trục hoành, với x ∈ [0; 4].

Diện tích cần tính là:

S = $\underset{0}{\overset{4}{\int }}\left|\sqrt{\mathrm{x}}-\frac{{\mathrm{x}}^2}{8}\right|\mathrm{d}\mathrm{x}=\underset{0}{\overset{4}{\int }}\left(\sqrt{\mathrm{x}}-\frac{{\mathrm{x}}^2}{8}\right)\mathrm{d}\mathrm{x}=\left(\frac{2}{3}\mathrm{x}\sqrt{\mathrm{x}}-\frac{{\mathrm{x}}^3}{24}\right){|}_0^4=\frac{8}{3}$.

b) Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = $\sqrt{\mathrm{x}}$, y = 0, x = 0, x = 4 quanh trục Ox là:

V₁ = $\mathrm{\pi }\underset{0}{\overset{4}{\int }}{\left(\sqrt{\mathrm{x}}\right)}^2\mathrm{d}\mathrm{x}=\mathrm{\pi }\underset{0}{\overset{4}{\int }}\mathrm{x}\mathrm{d}\mathrm{x}=\frac{\mathrm{\pi }{\mathrm{x}}^2}{2}{|}_0^4=8\mathrm{\pi }.$

Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = $\frac{{\mathrm{x}}^2}{8}$, y = 0, x = 0, x = 2 quanh trục Ox là:

V₂ = $\mathrm{\pi }\underset{0}{\overset{4}{\int }}{\left(\frac{{\mathrm{x}}^2}{8}\right)}^2\mathrm{d}\mathrm{x}=\mathrm{\pi }\underset{0}{\overset{4}{\int }}\frac{{\mathrm{x}}^4}{64}\mathrm{d}\mathrm{x}=\frac{\mathrm{\pi }{\mathrm{x}}^5}{320}{|}_0^4=\frac{16\mathrm{\pi }}{5}.$

Thể tích cần tính là:

V = V₁ – V₂ = $8\mathrm{\pi }-\frac{16\mathrm{\pi }}{5}=\frac{24\mathrm{\pi }}{5}$.

Lời giải Sách bài tập Toán lớp 12 Bài 13: Ứng dụng hình học của tích phân hay khác:

• Bài 4.21 trang 17 SBT Toán 12 Tập 2: Tính diện tích của các hình phẳng được tô màu dưới đây: ....

• Bài 4.22 trang 17 SBT Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi các đường sau: ....

• Bài 4.23 trang 17 SBT Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi các đường sau: ....

• Bài 4.24 trang 17 SBT Toán 12 Tập 2: Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường ....

• Bài 4.26 trang 18 SBT Toán 12 Tập 2: Tính thể tích của vật thể ℬ, biết đáy của ℬ là hình tròn bán kính 2 ....

• Bài 4.27 trang 18 SBT Toán 12 Tập 2: Hàm cầu và hàm cung của một sản phẩm được mô hình hóa bởi: ....

• Bài 4.28 trang 18 SBT Toán 12 Tập 2: Chi phí nhiên liệu dự kiến C (tính bằng triệu đô la mỗi năm) khi sử dụng một loại xe ....

• Bài 4.29 trang 18 SBT Toán 12 Tập 2: Doanh thu từ một quy trình sản xuất (tính bằng triệu đô la mỗi năm) ....

• Bài 4.30 trang 18 SBT Toán 12 Tập 2: Một trận dịch lây lan đến mức sau khi bùng phát t tuần số người nhiễm bệnh là: ....