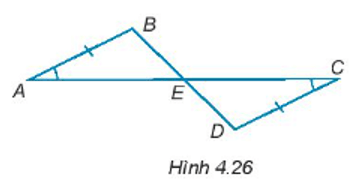
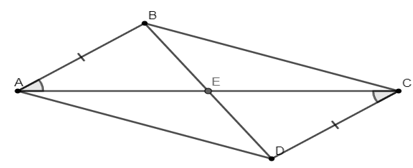
Cho các điểm A, B, C, D, E như Hình 4.26, biết rằng AB = CD, ∠BAE = ∠DCE. Chứng minh rằng

Cho các điểm A, B, C, D, E như Hình 4.26, biết rằng AB = CD, . Chứng minh rằng:

Giải SBT Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 4.26 trang 61 sách bài tập Toán lớp 7 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.26, biết rằng AB = CD, $\widehat{BAE}=\widehat{DCE}$. Chứng minh rằng:

a) E là trung điểm của các đoạn thẳng AC và BD.

b) ∆ACD = ∆CAB.

c) AD song song với BC.

Lời giải:

a) Xét tam giác ABE có:

$\widehat{BAE}+\widehat{ABE}+\widehat{AEB}=180°$

$\widehat{ABE}=180°-\widehat{BAE}-\widehat{AEB}$ (1)

Xét tam giác CDE có:

$\widehat{DCE}+\widehat{DEC}+EDC=180°$

$\widehat{EDC}=180°-\widehat{DCE}-\widehat{DEC}$ (2)

Mà $\widehat{BAE}=\widehat{DCE}$ (giả thiết); $\widehat{AEB}=\widehat{DEC}$ (hai góc đối đỉnh) (3)

Từ (1), (2), (3) ta suy ra $\widehat{ABE}=\widehat{EDC}$.

Xét ∆ABE và ∆CDE có:

$\widehat{ABE}=\widehat{EDC}$ (chứng minh trên)

AB = CD (giả thiết)

 $\widehat{BAE}=\widehat{DCE}$ (giả thiết)

Do đó, ∆ABE = ∆CDE (g – c – g).

Suy ra, AE = CE; BE = DE (các cặp cạnh tương ứng)

Vì AE = CE và E nằm giữa A và C nên E là trung điểm của AC;

Vì BE = DE và B nằm giữa D và B nên E là trung điểm của BD.

b) Xét ∆ACD và ∆CAB có:

CD = AB (giả thiết)

AC chung

$\widehat{BAC}=\widehat{DCA}$ (giả thiết)

Do đó, ∆ACD = ∆CAB (c – g – c).

c) Vì ∆ACD = ∆CAB nên $\widehat{DAC}=\widehat{BCA}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong nên AD song song với BC.