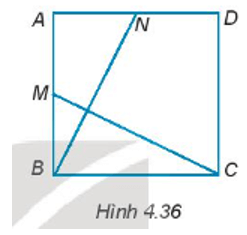
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36)
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.
Giải SBT Toán 7 Kết nối tri thức Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 4.34 trang 65 sách bài tập Toán lớp 7 Tập 1: Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.
Lời giải:
Vì ABCD là hình vuông nên AB = BC = CD = DA.
Vì N là trung điểm của AD nên AN = ND = .
Vì M là trung điểm của AB nên AM = MB = .
Mà AB = AD nên AN = BM.
Xét ∆ANB và ∆BMC có:
AN = BM (chứng minh trên)
AB = BC (chứng minh trên)
= 90° (do ABCD là hình vuông)
Do đó, ∆ANB = ∆BMC (hai cạnh góc vuông)
Suy ra, BN = CM (hai cạnh tương ứng).
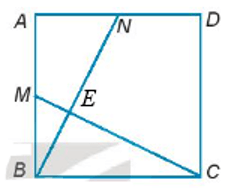
Gọi E là giao điểm của BN và CM.
Do ∆ANB = ∆BMC nên .
Từ định lí tổng ba góc trong tam giác BME và tam giác ABN, ta suy ra:
.
Vậy BN vuông góc với CM tại E.