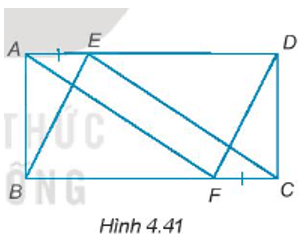
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41)

Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:

Giải SBT Toán 7 Kết nối tri thức Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 4.39 trang 66 sách bài tập Toán lớp 7 Tập 1: Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:

a) AF = CE.

b) AF // CE.

Lời giải:

a) Vì ABCD là hình chữ nhật nên AD = BC; AB = CD.

Ta có: AD = AE + ED; BC = BF + FC mà FC = AE (gt) và AD = BC nên ED = BF.

Vì ABCD là hình chữ nhật nên $\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=\widehat{DAB}=90°$.

Xét ∆ABF và ∆CDE có:

AB = CD (chứng minh trên)

BF = ED (chứng minh trên)

$\widehat{ABF}=\widehat{CDE}=90°$ (do $\widehat{ABC}=\widehat{CDA}=90°$)

Do đó, ∆ABF = ∆CDE (hai cạnh góc vuông).

Suy ra, AF = CE.

b) Vì ∆ABF = ∆CDE nên $\widehat{AFB}=\widehat{CED}$ (hai góc tương ứng).

Lại có ABCD là hình chữ nhật nên AD // BC nên $\widehat{CED}=\widehat{ECF}$ (hai góc so le trong).

Ta có: $\widehat{AFB}=\widehat{CED}$; $\widehat{CED}=\widehat{ECF}$ nên $\widehat{AFB}=\widehat{ECF}$.

Mà hai góc này ở vị trí đồng vị

Nên AF // CE (điều phải chứng minh).