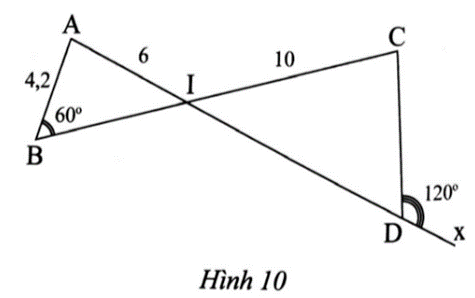
Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; góc ABI = 60 độ; góc CDx = 120 độ

Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; = 60°; = 120°. Tính độ dài CD.

Giải sách bài tập Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác - Chân trời sáng tạo

Bài 10 trang 64 sách bài tập Toán 8 Tập 2: Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; $\widehat{ABI}$ = 60°; $\widehat{CDx}$ = 120°. Tính độ dài CD.

Lời giải:

Ta có $\widehat{CDx}+\widehat{CDI}=180°$ (hai góc kề bù).

Suy ra $\widehat{CDI}=180°-\widehat{CDI}$ = 180° - 120° = 60°.

Xét ∆IAB và ∆ICD có

$\widehat{ABI}=\widehat{CDI}$ (= 60°) và $\widehat{AIB}=\widehat{CID}$ (đối đỉnh).

Suy ra  ∆IAB ᔕ ∆ICD (g.g).

Suy ra $\frac{IA}{IC}=\frac{AB}{CD}$ hay $\frac{6}{10}=\frac{4,2}{CD}$.

Do đó $CD=\frac{4,2.10}{6}=7$.

Vậy CD = 7.

Lời giải SBT Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác hay khác:

• Bài 1 trang 62 sách bài tập Toán 8 Tập 2: Tam giác ABC có độ dài AB = 9 cm, AC = 12 cm, BC = 14 cm. Tam giác A'B'C' đồng dạng với tam giác ABC ...

• Bài 2 trang 62 sách bài tập Toán 8 Tập 2: a) Tam giác ABC và MBN (Hình 4) có đồng dạng với nhau không? Vì sao? ...

• Bài 3 trang 63 sách bài tập Toán 8 Tập 2: Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm, AB = 8 cm, NA = 12 cm, NB = 6,4 cm. Chứng minh rằng: ...

• Bài 4 trang 63 sách bài tập Toán 8 Tập 2: Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng với nhau (Hình 6). Bồn hoa thứ nhất có chu vi 7,5 m ...

• Bài 5 trang 63 sách bài tập Toán 8 Tập 2: Quan sát Hình 7. Chứng minh rằng $\widehat{OBA}=\widehat{OAC}$. ...

• Bài 6 trang 63 sách bài tập Toán 8 Tập 2: Quan sát Hình 8. a) Chứng minh rằng ∆ABC ᔕ ∆DEF ...

• Bài 7 trang 63 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6 ...

• Bài 8 trang 64 sách bài tập Toán 8 Tập 2: Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB ...

• Bài 9 trang 64 sách bài tập Toán 8 Tập 2: Quan sát Hình 9. a) Chứng minh rằng ∆ABC ᔕ ∆MNQ ...

• Bài 11 trang 64 sách bài tập Toán 8 Tập 2: Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, $\widehat{N}=45°$, $\widehat{P}=75°$ ...

• Bài 12 trang 64 sách bài tập Toán 8 Tập 2: Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của $\widehat{ADC}$ và $\widehat{DAB}=\widehat{DBC}$. Chứng minh rằng: ...

• Bài 13 trang 65 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho $\widehat{ADE}=\widehat{ACB}$ ...