Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của
Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của và . Chứng minh rằng:
Giải sách bài tập Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác - Chân trời sáng tạo
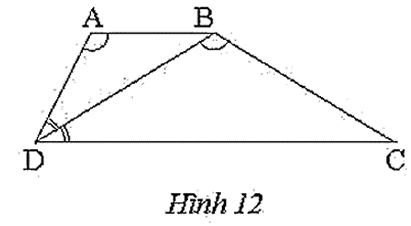
Bài 12 trang 64 sách bài tập Toán 8 Tập 2: Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của và . Chứng minh rằng:
a) ∆ABD ᔕ ∆BDC.
b) BD2 = AB . DC.
Lời giải:
a) Xét ∆ABD và ∆BDC có
và (DB là tia phân giác của ).
Do đó ∆ABD ᔕ ∆BDC (g.g).
b) Ta có ∆ABD ᔕ ∆BDC, suy ra .
Do đó BD2 = AB . DC (đpcm).
Lời giải SBT Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác hay khác:
Bài 5 trang 63 sách bài tập Toán 8 Tập 2: Quan sát Hình 7. Chứng minh rằng . ...
Bài 6 trang 63 sách bài tập Toán 8 Tập 2: Quan sát Hình 8. a) Chứng minh rằng ∆ABC ᔕ ∆DEF ...