Cho tứ giác EKIT có EK = ET, IK = IT

Cho tứ giác EKIT có EK = ET, IK = IT; . Gọi S là giao điểm của hai đường chéo. Tìm số đo các góc .

Giải SBT Toán 8 Bài tập cuối chương 3 - Chân trời sáng tạo

Bài 12 trang 74 sách bài tập Toán 8 Tập 1: Cho tứ giác EKIT có EK = ET, IK = IT; $\hat{K E T} = 90 °; \hat{E K I} = 105 °$ . Gọi S là giao điểm của hai đường chéo. Tìm số đo các góc $\hat{K I S}, \hat{S K I}$ .

Lời giải:

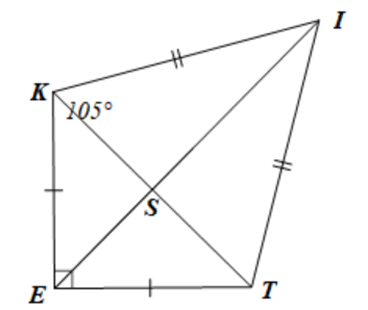
Xét ∆KEI và ∆TEI có:

EK = ET, IK = IT; cạnh EI chung

Suy ra ∆KEI = ∆TEI (c.c.c)

Do đó $\hat{K E T} = \hat{T E I}$ hay $\hat{K E S} = \hat{T E S} = \frac{\hat{K E T}}{2} = \frac{90 °}{2} = 45 °$ .

Vì tổng ba góc trong một tam giác bằng 180° nên ta có:

$\hat{K E I} + \hat{K I E} + \hat{E K I} = 180 °$

Suy ra $\hat{K I E} = 180 ° - \hat{K E I} - \hat{E K I} = 180 ° - 45 ° - 105 ° = 30 °$ .

Xét ∆KET có EK = ET nên ∆KET cân tại E

Lại có $\hat{K E T} = 90 °$ nên ∆KET vuông cân tại E

Do đó $\hat{E K T} = 45 °$

Khi đó $\hat{S K I} = \hat{E K I} - \hat{E K T} = 105 ° - 45 ° = 60 °$ .

Lời giải SBT Toán 8 Bài tập cuối chương 3 hay khác:

Xem thêm giải sách bài tập Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Sách bài tập Toán 8

Cho tứ giác EKIT có EK = ET, IK = IT

Giải SBT Toán 8 Bài tập cuối chương 3 - Chân trời sáng tạo

Xem thêm giải sách bài tập Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: