Cho hình thang cân có độ dài hai đáy lần lượt là 10 cm và 4 cm

Cho hình thang cân có độ dài hai đáy lần lượt là 10 cm và 4 cm, độ dài cạnh bên là 5 cm. Hình thang đó có chiều cao là

Giải SBT Toán 8 Bài tập cuối chương 3 - Chân trời sáng tạo

Câu 4 trang 72 sách bài tập Toán 8 Tập 1: Cho hình thang cân có độ dài hai đáy lần lượt là 10 cm và 4 cm, độ dài cạnh bên là 5 cm. Hình thang đó có chiều cao là

A. 2 cm.

B. 3 cm.

C. 4 cm.

D. 6 cm.

Lời giải:

Đáp án đúng là: C

Giả sử ABCD hình thang cân (AB // CD) có AB = 4 cm, CD = 10 cm và AD = BC = 5 cm (hình vẽ).

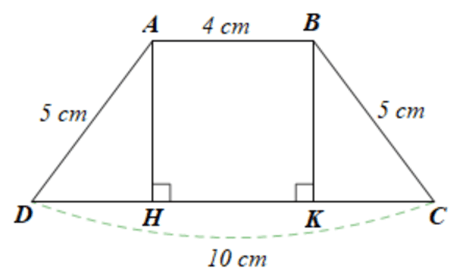
Kẻ hai đường cao AH và BK.

Xét ∆ADH vuông tại H và ∆BCK vuông tại K có:

AD = BC (hai cạnh bên bằng nhau của hình thang cân ABCD)

$\widehat{ADH}=\widehat{BCK}$ (do ABCD là hình thang cân)

Suy ra ∆ADH = ∆BCK (cạnh huyền – góc nhọn)

Do đó DH = CK (hai cạnh tương ứng)

Ta có: ABKH là hình chữ nhật nên AB = HK = 4 cm.

Mà DH + HK + CK = DC, suy ra $DH=CK=\frac{CD-HK}{2}=\frac{10-4}{2}=3$ (cm).

Áp dụng định lý Pythagore trong ∆ADH vuông tại H ta có:

AD² = AH² + DH², suy ra AH² = AD² ‒ DH² = 5² ‒ 3² = 16

Suy ra $AH=\sqrt{16}=4$ (cm).

Lời giải SBT Toán 8 Bài tập cuối chương 3 hay khác:

• Câu 1 trang 72 sách bài tập Toán 8 Tập 1: Cho tam giác MNP vuông tại M. Biết MN = 40, MP = 9. Độ dài cạnh NP bằng ...

• Câu 2 trang 72 sách bài tập Toán 8 Tập 1: Ba số nào sau đây không thể là độ dài ba cạnh của một tam giác vuông? ...

• Câu 3 trang 72 sách bài tập Toán 8 Tập 1: Một tứ giác có số đo ba góc lần lượt bằng 80°, 40°, 100°. Số đo góc còn lại bằng ...

• Câu 5 trang 72 sách bài tập Toán 8 Tập 1: Cho hình bình hành MNPQ có O là giao điểm của hai đường chéo. Biết MN = 6, OM = 3, ON = 4. Độ dài của MP, NQ, PQ lần lượt là ...

• Câu 6 trang 73 sách bài tập Toán 8 Tập 1: Cho hình thoi EFGH có hai đường chéo cắt nhau tại O. Biết OE = 6, OF = 8. Độ dài cạnh EF là ...

• Câu 7 trang 73 sách bài tập Toán 8 Tập 1: Một hình vuông có diện tích bằng diện tích của hình chữ nhật có hai cạnh bằng 2 cm và 18 cm. Độ dài cạnh của hình vuông bằng ...

• Câu 8 trang 73 sách bài tập Toán 8 Tập 1: Một hình vuông có cạnh bằng $\sqrt{8}$ cm. Độ dài đường chéo của hình vuông bằng ...

• Câu 9 trang 73 sách bài tập Toán 8 Tập 1: Một hình bình hành có thể không có tính chất nào sau đây? ...

• Bài 10 trang 73 sách bài tập Toán 8 Tập 1: Tính độ dài cạnh chưa biết của các tam giác vuông trong Hình 1 ...

• Bài 11 trang 73 sách bài tập Toán 8 Tập 1: Tìm số đo các góc chưa biết của các tứ giác trong Hình 2 ...

• Bài 12 trang 74 sách bài tập Toán 8 Tập 1: Cho tứ giác EKIT có EK = ET, IK = IT; $\widehat{KET}=90°;\widehat{EKI}=105°$. Gọi S là giao điểm của hai đường chéo. Tìm số đo các góc $\widehat{KIS},\widehat{SKI}$ ...

• Bài 13 trang 74 sách bài tập Toán 8 Tập 1: Tính chiều cao của hình thang cân ABCD biết rằng cạnh bên BC = 25 cm và các cạnh đáy AB = 10 cm, CD = 24 cm ...

• Bài 14 trang 74 sách bài tập Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, DB là tia phân giác của góc D, DB ⊥ BC. Biết AB = 4 cm. Tính chu vi hình thang đó ...

• Bài 15 trang 74 sách bài tập Toán 8 Tập 1: Cho tam giác ABC cân tại A có BC = 6 cm. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC ...

• Bài 16 trang 74 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho BM = DN ...

• Bài 17 trang 74 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Lấy các điểm M, N, P, Q lần lượt là trung điểm của AO, BO, CO, DO ...

• Bài 18 trang 74 sách bài tập Toán 8 Tập 1: Cho hình chữ nhật ABCD có AB = 2BC. Gọi I là trung điểm của AB và K là trung điểm của CD ...

• Bài 19 trang 74 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc $\widehat{ADB},\widehat{DBC}$(E ∈ AB, K ∈ CD) ...