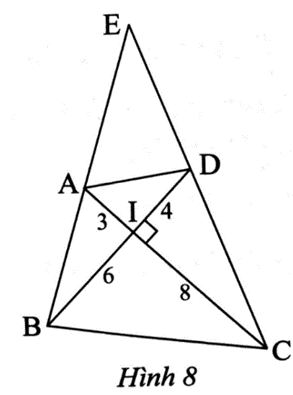
Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC vuông góc BD

Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC ⊥ BD, chứng minh rằng:

Giải sách bài tập Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông - Chân trời sáng tạo

Bài 4 trang 68 sách bài tập Toán 8 Tập 2: Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC ⊥ BD, chứng minh rằng:

a) ∆AIB ᔕ ∆DIC.

b) EA . EB = EC . ED.

Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC vuông góc BD

Lời giải:

a) Ta có $\frac{I A}{I D} = \frac{3}{4}$ ; $\frac{I B}{I C} = \frac{6}{8} = \frac{3}{4}$ suy ra $\frac{I A}{I D} = \frac{I B}{I C}$ .

Xét ∆AIB vuông tại I và ∆DIC vuông tại I có $\frac{I A}{I D} = \frac{I B}{I C}$ .

Suy ra ∆AIB ᔕ ∆DIC

b) Ta có ∆AIB ᔕ ∆DIC, suy ra $\hat{A B I} = \hat{D C I}$ .

Xét ∆EDB và ∆EAC có

$\hat{E}$ chung và $\hat{A B I} = \hat{D C I}$ .

Do đó ∆EDB ᔕ ∆EAC (g.g).

Suy ra $\frac{E D}{E A} = \frac{E B}{E C}$ . Do đó EA . EB = EC . ED (đpcm).

Lời giải SBT Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông hay khác: