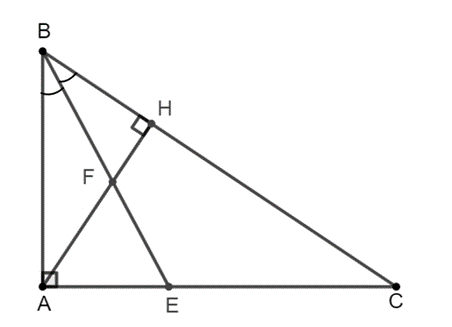
Cho tam giác ABC vuông tại A (AB < AC) và kẻ đường cao AH
Cho tam giác ABC vuông tại A (AB < AC) và kẻ đường cao AH. Tia phân giác của cắt AC tại E và cắt AH tại F. Chứng minh rằng:
Giải sách bài tập Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông - Chân trời sáng tạo
Bài 8 trang 69 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB < AC) và kẻ đường cao AH. Tia phân giác của cắt AC tại E và cắt AH tại F. Chứng minh rằng:
a) AB . HF = AE . HB.
b) AE = AF.
c) AE2 = EC . FH.
Lời giải:
a) Vì BE là tia phân giác của nên .
Xét ∆ABE vuông tại A và ∆HBF vuông tại H có
()
Do đó ∆ABE ᔕ ∆HBF (g.g)
Suy ra . Do đó AB . HF = AE . HB (đpcm).
b) Ta có ∆ABE ᔕ ∆HBF.
Suy ra hay (các góc tương ứng).
Mà (đối đỉnh) nên . Suy ra ∆AEF cân tại A.
Do đó AE = AF.
c) Xét ∆ABC có BE là tia phân giác của , suy ra (1)
Xét ∆ABH có BF là tia phân giác của , suy ra (2)
Xét ∆ABH vuông tại H và ∆ABC vuông tại A có chung.
Do đó ∆ABH ᔕ ∆CBA, suy ra (3)
Từ (1); (2) và (3) suy ra .
Do đó AE . AF = EC . FH.
Mà AE = AF, suy ra AE2 = EC . FH (đpcm).
Lời giải SBT Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông hay khác: