Cho ∆ABC đều, cạnh 3 cm M, N lần lượt là trung điểm của AB và AC

Cho ∆ABC đều, cạnh 3 cm; M, N lần lượt là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng

Giải sách bài tập Toán 8 Bài tập cuối chương 4 - Kết nối tri thức

Câu 10 trang 54 sách bài tập Toán 8 Tập 1: Cho ∆ABC đều, cạnh 3 cm; M, N lần lượt là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng

A. 8 cm.

B. 7,5 cm.

C. 6 cm.

D. 7 cm.

Lời giải:

Đáp án đúng là: B

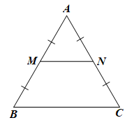
Cho ∆ABC đều, cạnh 3 cm M, N lần lượt là trung điểm của AB và AC

Trong ∆ABC có M, N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của ∆ABC

Suy ra $M N = \frac{1}{2} B C$ (tính chất đường trung bình của tam giác)

Hay $M N = \frac{1}{2} \cdot 3 = 1,5$ (cm)

Do ∆ABC đều nên AB = AC

Lại có M, N lần lượt là trung điểm của AB và AC nên $B M = \frac{1}{2} A B = \frac{1}{2} A C = C N$

Hay $B M = C N = \frac{1}{2} \cdot 3 = 1,5$ (cm).

Vậy chu vi của tứ giác BMNC là:

BM + MN + NC + BC = 1,5 + 1,5 + 1,5 + 3 = 7,5 (cm).

Lời giải SBT Toán 8 Bài tập cuối chương 4 hay khác: