Cho đường tròn (O; R) và điểm A sao cho OA = 2R, Kẻ tiếp tuyến AB của đường tròn (O; R)

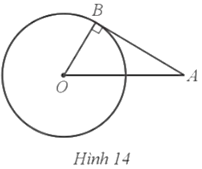
Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (Hình 14). Tính độ dài đoạn thẳng AB theo R.

Giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn - Cánh diều

Bài 14 trang 106 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (Hình 14). Tính độ dài đoạn thẳng AB theo R.

Lời giải:

Do AB của đường tròn (O; R) với B là tiếp điểm nên OB ⊥ AB tại B.

Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có:

OA² = OB² + AB²

Suy ra $AB=\sqrt{O{A}^2-O{B}^2}=\sqrt{{\left(2R\right)}^2-R^2}=\sqrt{3R^2}=R\sqrt{3}.$

Vậy $AB=R\sqrt{3}.$

Lời giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn hay khác:

• Bài 11 trang 105 SBT Toán 9 Tập 1: Cho đường thẳng a và điểm O với khoảng cách từ điểm O đến đường thẳng a là 1 cm. Vẽ đường tròn tâm O bán kính 3 cm. ....

• Bài 12 trang 106 SBT Toán 9 Tập 1: Cho $\widehat{xOy}=30°$ và điểm O’ thuộc tia Ox sao cho OO’ = 4 cm. a) Tính khoảng cách từ điểm O’ đến tia Oy. ....

• Bài 13 trang 106 SBT Toán 9 Tập 1: Cho hình thang vuông ABCD $\left(\widehat{A}=\widehat{D}=90°\right)$ có AB = 4 cm, BC = 13 cm, CD = 9 cm. ....

• Bài 15 trang 106 SBT Toán 9 Tập 1: Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, ....

• Bài 16 trang 106 SBT Toán 9 Tập 1: Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O. ....

• Bài 17 trang 106 SBT Toán 9 Tập 1: Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB của đường tròn với B là tiếp điểm. Lấy các điểm C, D thuộc đường tròn (O) sao cho C nằm giữa A và D, ....

• Bài 18 trang 107 SBT Toán 9 Tập 1: Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A ....