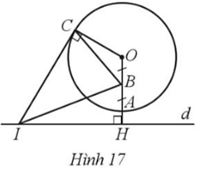
Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm

Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I.

Giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn - Cánh diều

Bài 18 trang 107 SBT Toán 9 Tập 1: Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I.

Lời giải:

Do B là trung điểm của OA nên $OB=AB=\frac{OA}{2}.$

Ta có: $BH=OH-OB=OH-\frac{OA}{2}=5-\frac{4}{2}=3\text{ (cm).}$

Do OH là khoảng cách từ O đến đường thẳng d nên OH ⊥ d tại H.

Xét ∆IBH vuông tại H, theo định lí Pythagore, ta có:

IB² = IH² + BH² = IH² + 3² = IH² + 9.

Xét ∆OIH vuông tại H, theo định lí Pythagore, ta có: OI² = OH² + IH².

Do tiếp tuyến IC của đường tròn (O) với C là tiếp điểm nên OC ⊥ IC tại C.

Xét ∆ICO vuông tại C, theo định lí Pythagore, ta có: IO² = IC² + OC².

Suy ra IC² = IO² ‒ OC² = (OH² + IH²) ‒ OC² = (5² + IH²) ‒ 4² = IH² + 9.

Do đó IB² = IC² (vì cùng bằng IH² + 9).

Vậy IB = IC hay tam giác IBC cân tại I.

Lời giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn hay khác:

• Bài 11 trang 105 SBT Toán 9 Tập 1: Cho đường thẳng a và điểm O với khoảng cách từ điểm O đến đường thẳng a là 1 cm. Vẽ đường tròn tâm O bán kính 3 cm. ....

• Bài 12 trang 106 SBT Toán 9 Tập 1: Cho $\widehat{xOy}=30°$ và điểm O’ thuộc tia Ox sao cho OO’ = 4 cm. a) Tính khoảng cách từ điểm O’ đến tia Oy. ....

• Bài 13 trang 106 SBT Toán 9 Tập 1: Cho hình thang vuông ABCD $\left(\widehat{A}=\widehat{D}=90°\right)$ có AB = 4 cm, BC = 13 cm, CD = 9 cm. ....

• Bài 14 trang 106 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (Hình 14). Tính độ dài đoạn thẳng AB theo R. ....

• Bài 15 trang 106 SBT Toán 9 Tập 1: Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, ....

• Bài 16 trang 106 SBT Toán 9 Tập 1: Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O. ....

• Bài 17 trang 106 SBT Toán 9 Tập 1: Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB của đường tròn với B là tiếp điểm. Lấy các điểm C, D thuộc đường tròn (O) sao cho C nằm giữa A và D, ....