Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O

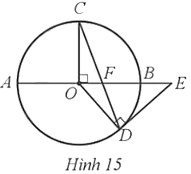
Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (Hình 15). Chứng minh EF = ED.

Giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn - Cánh diều

Bài 15 trang 106 SBT Toán 9 Tập 1: Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (Hình 15). Chứng minh EF = ED.

Lời giải:

Do OC = OD nên ∆OCD cân tại O, suy ra $\widehat{OCD}=\widehat{ODC}$ hay $\widehat{OCF}=\widehat{ODF}.$

Xét ∆COF vuông tại O có $\widehat{OCF}+\widehat{OFC}=90°$ (tổng hai góc nhọn trong)

Lại có $\widehat{OFC}=\widehat{DFE}$ (đối đỉnh)

Suy ra $\widehat{ODF}+\widehat{DFE}=90°$

Mà $\widehat{ODF}+\widehat{FDE}=90°$ nên $\widehat{DFE}=\widehat{FDE}.$

Do đó ∆EDF cân tại E, suy ra EF = ED.

Lời giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn hay khác:

• Bài 11 trang 105 SBT Toán 9 Tập 1: Cho đường thẳng a và điểm O với khoảng cách từ điểm O đến đường thẳng a là 1 cm. Vẽ đường tròn tâm O bán kính 3 cm. ....

• Bài 12 trang 106 SBT Toán 9 Tập 1: Cho $\widehat{xOy}=30°$ và điểm O’ thuộc tia Ox sao cho OO’ = 4 cm. a) Tính khoảng cách từ điểm O’ đến tia Oy. ....

• Bài 13 trang 106 SBT Toán 9 Tập 1: Cho hình thang vuông ABCD $\left(\widehat{A}=\widehat{D}=90°\right)$ có AB = 4 cm, BC = 13 cm, CD = 9 cm. ....

• Bài 14 trang 106 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (Hình 14). Tính độ dài đoạn thẳng AB theo R. ....

• Bài 16 trang 106 SBT Toán 9 Tập 1: Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O. ....

• Bài 17 trang 106 SBT Toán 9 Tập 1: Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB của đường tròn với B là tiếp điểm. Lấy các điểm C, D thuộc đường tròn (O) sao cho C nằm giữa A và D, ....

• Bài 18 trang 107 SBT Toán 9 Tập 1: Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A ....