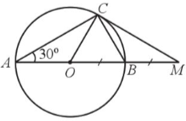
Cho đường tròn (O; R) có đường kính AB, Vẽ dây AC sao cho góc CAB = 30 độ

Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh:

Giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn - Cánh diều

Bài 21 trang 109 SBT Toán 9 Tập 1: Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho $\widehat{CAB}=30°.$ Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh:

a) MC là tiếp tuyến của đường tròn (O);

b) $MC=R\sqrt{3}.$

Lời giải:

a) Ta có C nằm trên đường tròn (O) đường kính AB nên $OC=\frac{1}{2}AB.$

Xét ∆ABC có CO là trung tuyến ứng với cạnh AB và $OC=\frac{1}{2}AB$ nên tam giác ABC vuông tại C, hay $\widehat{ACB}=90°.$

Ta có ∆OAC cân tại O (do OA = OC = R) nên $\widehat{OCA}=\widehat{OAC}=30°.$

Mà $\widehat{ACB}=\widehat{OCA}+\widehat{OCB}$ nên $\widehat{OCB}=\widehat{ACB}-\widehat{OCA}=90°-30°=60°.$

Xét ∆OBC cân tại O (do OB = OC = R) có $\widehat{OCB}=60°$ nên ∆OBC là tam giác đều

Suy ra CB = OB.

Mà B là trung điểm của OM nên $OB=\frac{OM}{2},$ suy ra $CB=\frac{OM}{2}.$

Xét ∆COM có CB là trung tuyến ứng với cạnh OM và $CB=\frac{OM}{2}$ nên tam giác COM vuông tại C, hay MC ⊥ OC tại C nằm trên đường tròn (O; R).

Vậy MC là tiếp tuyến của đường tròn (O).

b) Ta có B là trung điểm của OM nên OM = 2OB = 2R.

Xét ∆COM vuông tại C, theo định lí Pythagore, ta có: OM² = OC² + MC²

Suy ra $MC=\sqrt{O{M}^2-O{C}^2}=\sqrt{{\left(2R\right)}^2-R^2}=\sqrt{3R^2}=R\sqrt{3}.$

Lời giải SBT Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn hay khác:

• Bài 19 trang 108 SBT Toán 9 Tập 1: Cho đường tròn tâm O bán kính 15 cm. Điểm A nằm ngoài đường tròn sao cho OA = 25 cm. Kẻ tiếp tuyến AB của đường tròn (O). ....

• Bài 20 trang 109 SBT Toán 9 Tập 1: Cho đường tròn (O) và dây AB khác đường kính. Kẻ bán kính OC đi qua trung điểm I của đoạn thẳng AB. Vẽ đường tròn (C; CI). ....

• Bài 22 trang 109 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và điểm A nằm trên đường tròn. Lấy điểm B sao cho A là trung điểm của đoạn thẳng OB. Kẻ hai tiếp tuyến BM, BN của đường tròn (O). ....

• Bài 23 trang 109 SBT Toán 9 Tập 1: Hình 23 minh hoạ thước phân giác. Thước gồm hai thanh gỗ ghép lại thành góc vuông BAC và một tấm gỗ có dạng hình tam giác ACD với AD là tia phân giác của góc BAC. ....

• Bài 24 trang 109 SBT Toán 9 Tập 1: Cho nửa đường tròn tâm O đường kính AB. Kẻ các tiếp tuyến Ax, By của đường tròn (O). Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt Ax, By lần lượt tại C, ....

• Bài 25 trang 109 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài với nhau tại A với R ≠ r. Đường nối OO’ lần lượt cắt hai đường tròn (O) và (O’) tại B và C. ....

• Bài 26 trang 109 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH. Hình chiếu của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB ....