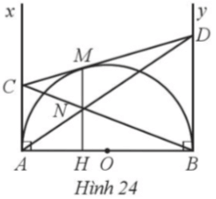
Cho nửa đường tròn tâm O đường kính AB, Kẻ các tiếp tuyến Ax, By của đường tròn
Cho nửa đường tròn tâm O đường kính AB. Kẻ các tiếp tuyến Ax, By của đường tròn (O). Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt Ax, By lần lượt tại C, D. Gọi N là giao điểm của AD và BC và H là giao điểm của MN và AB (Hình 24). Chứng minh:
Giải SBT Toán 9 Bài 3: Tiếp tuyến của đường tròn - Cánh diều
Bài 24 trang 109 SBT Toán 9 Tập 1: Cho nửa đường tròn tâm O đường kính AB. Kẻ các tiếp tuyến Ax, By của đường tròn (O). Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt Ax, By lần lượt tại C, D. Gọi N là giao điểm của AD và BC và H là giao điểm của MN và AB (Hình 24). Chứng minh:
a) MN ⊥ AB;
b) MN = NH.
Lời giải:
a) Do Ax, By là tiếp tuyến của đường tròn tâm O đường kính AB nên Ax ⊥ AB, By ⊥ AB, suy ra Ax // By.
Đường tròn (O) có:
⦁ hai tiếp tuyến Ax, CD cắt nhau tại C nên CA = CM;
⦁ hai tiếp tuyến By, CD cắt nhau tại D nên DB = DM.
Xét ∆ANC có AC // BD nên (hệ quả định lí Thalès) suy ra
Do đó MN // AC (định lí Thalès đảo) hay MN // Ax
Mà Ax ⊥ AB nên MN ⊥ AB.
b) Xét ∆ACD có MN // AC nên (hệ quả của định lí Thalès).
Xét ∆ANC có AC // BD nên (hệ quả của định lí Thalès).
Suy ra (tính chất tỉ lệ thức) hay
Xét ∆ABC có NH // AC nên (hệ quả của định lí Thalès).
Do đó, ta có:
Vậy MN = NH.
Lời giải SBT Toán 9 Bài 3: Tiếp tuyến của đường tròn hay khác: