Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài với nhau tại A với R ≠ r
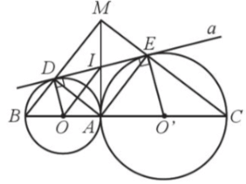
Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài với nhau tại A với R ≠ r. Đường nối OO’ lần lượt cắt hai đường tròn (O) và (O’) tại B và C. Đường thẳng a lần lượt tiếp xúc với hai đường tròn (O) và (O’) tại D và E. Gọi M là giao điểm của BD và CE. Chứng minh:
Giải SBT Toán 9 Bài 3: Tiếp tuyến của đường tròn - Cánh diều
Bài 25 trang 109 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài với nhau tại A với R ≠ r. Đường nối OO’ lần lượt cắt hai đường tròn (O) và (O’) tại B và C. Đường thẳng a lần lượt tiếp xúc với hai đường tròn (O) và (O’) tại D và E. Gọi M là giao điểm của BD và CE. Chứng minh:
a)
b) MA tiếp xúc với hai đường tròn (O) và (O’);
c) MD.MB = ME.MC.
Lời giải:
a) Ta có đường thẳng a là tiếp tuyến của đường tròn (O) tại D nên a ⊥ OD.
Đường thẳng a cũng là tiếp tuyến của đường tròn (O’) tại E nên a ⊥ O’E.
Suy ra OD // O’E nên (hai góc đồng vị). (1)
Ta có ∆OBD cân tại O (do OB = OD = R) nên
Mà nên (2)
Tương tự với ∆O’AE cân tại O’ (do O’A = O’E = r) ta có
Từ (1), (2) và (3) suy ra
Xét ∆O’CE cân tại O’ (do O’C = O’E = r) nên
Mà
Từ (4), (5) và (6) suy ra hay
Ta lại có (tổng ba góc của tam giác BCM)
Do đó hay
b) Xét ∆ABD có OA = OB = OD = R suy ra nên ∆ABD vuông tại D, hay AD ⊥ BM.
Tương tự, ta cũng chứng minh được DE ⊥ CM.
Xét tứ giác ADME có nên tứ giác ADME là hình chữ nhật.
Suy ra hai đường chéo AM và DE bằng nhau và chúng cắt nhau tại trung điểm I của mỗi đường, nên
Xét ∆OAI và ∆ODI có: OA = OD = R; IA = ID; OI là cạnh chung
Do đó ∆OAI = ∆ODI (c.c.c).
Suy ra hay MA vuông góc với BC tại điểm A nằm trên cả hai đường tròn (O) và (O’).
Vậy MA tiếp xúc với hai đường tròn (O) và (O’).
c) Ta có và nên
Lại có (chứng minh ở câu a) nên hay
Xét ∆BCM và ∆EDM có: là góc chung và
Do ∆BCM ᔕ ∆EDM (g.g) nên
Suy ra MD . MB = ME . MC.
Lời giải SBT Toán 9 Bài 3: Tiếp tuyến của đường tròn hay khác: