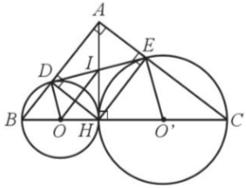
Cho tam giác ABC vuông tại A có đường cao AH, Hình chiếu của H trên AB, AC lần lượt là D, E
Cho tam giác ABC vuông tại A có đường cao AH. Hình chiếu của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB và (O’) là đường tròn đường kính HC. Chứng minh:
Giải SBT Toán 9 Bài 3: Tiếp tuyến của đường tròn - Cánh diều
Bài 26 trang 109 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH. Hình chiếu của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB và (O’) là đường tròn đường kính HC. Chứng minh:
a) Điểm D thuộc đường tròn (O) và điểm E thuộc đường tròn (O’);
b) Hai đường tròn (O) và (O’) tiếp xúc ngoài;
c) AH là tiếp tuyến chung của hai đường tròn (O) và (O’);
d) AH = DE;
e) Diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.
Lời giải:
a) Xét ∆BDH vuông tại D có đường trung tuyến DO ứng với cạnh huyền BH nên
Mà O là tâm đường tròn đường kính BH nên điểm D thuộc đường tròn (O).
Tương tự, ta chứng minh được nên điểm E thuộc đường tròn (O’).
b) Do OO’ = OH + O’H nên hai đường tròn (O) và (O’) tiếp xúc ngoài tại H.
c) Do AH vuông góc với OO’ tại H nên:
⦁ AH ⊥ HB tại H thuộc (O) nên AH là tiếp tuyến của đường tròn (O);
⦁ AH ⊥ HC tại H thuộc (O’) nên AH là tiếp tuyến của đường tròn (O’).
Vậy AH là tiếp tuyến chung của hai đường tròn (O) và (O’).
d) Xét tứ giác ADHE có nên tứ giác ADHE là hình chữ nhật. Suy ra AH = DE.
e) Do ADHE là hình chữ nhật nên hai đường chéo AH, DE bằng nhau và cắt nhau tại trung điểm I của mỗi đường. Do đó
Xét ∆ODI và ∆OHI có: ID = IH; OD = OH; OI là cạnh chung.
Do ∆ODI = ∆OHI (c.c.c) nên hay OD ⊥ DE.
Tương tự, ta chứng minh được O’E ⊥ DE.
Suy ra OD // O’E nên tứ giác DEO’O là hình thang có DE là đường cao.
Diện tích hình thang DEO’O là
Diện tích tam giác ABC là:
Mà DEư = AH và BC = BH + CH = 2OD + 2O’E = 2(OD + O’E).
Suy ra
Do đó
Vậy diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.
Lời giải SBT Toán 9 Bài 3: Tiếp tuyến của đường tròn hay khác: