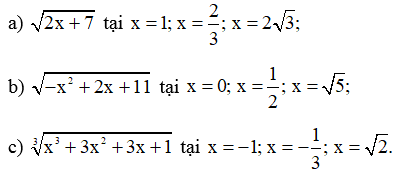Tính giá trị của mỗi biểu thức sau: căn bậc hai của (2x + 7) tại x= 1

Tính giá trị của mỗi biểu thức sau:

Giải SBT Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số - Cánh diều

Bài 24 trang 61 SBT Toán 9 Tập 1: Tính giá trị của mỗi biểu thức sau:

Lời giải:

a) Xét biểu thức $\sqrt{2x+7}.$

Thay x = 1 vào biểu thức trên, ta được:

$\sqrt{2\cdot 1+7}=\sqrt{2+7}=\sqrt{9}=3.$

Thay $x=\frac{2}{3}$ vào biểu thức trên, ta được:

$\sqrt{2\cdot \frac{2}{3}+7}=\sqrt{\frac{4}{3}+7}=\sqrt{\frac{25}{3}}=\frac{\sqrt{25}}{\sqrt{3}}=\frac{5}{\sqrt{3}}=\frac{5\sqrt{3}}{{\left(\sqrt{3}\right)}^2}=\frac{5\sqrt{3}}{3}.$

Thay $x=2\sqrt{3}$ vào biểu thức trên, ta được:

$\sqrt{2\cdot 2\sqrt{3}+7}=\sqrt{4\sqrt{3}+7}=\sqrt{2^2+2\cdot 2\cdot \sqrt{3}+{\left(\sqrt{3}\right)}^2}=\sqrt{{\left(2+\sqrt{3}\right)}^2}=2+\sqrt{3}.$

b) Xét biểu thức $\sqrt{-x^2+2x+11}$

Thay x = 0 vào biểu thức trên, ta được:

$\sqrt{-0^2+2\cdot 0+11}=\sqrt{11}.$

Thay $x=\frac{1}{2}$ vào biểu thức trên, ta được:

$\sqrt{-{\left(\frac{1}{2}\right)}^2+2\cdot \frac{1}{2}+11}=\sqrt{-\frac{1}{4}+1+11}=\sqrt{\frac{47}{4}}=\frac{\sqrt{47}}{\sqrt{4}}=\frac{\sqrt{47}}{2}.$

Thay $x=\sqrt{5}$ vào biểu thức trên, ta được:

$\sqrt{-{\left(\sqrt{5}\right)}^2+2\cdot \sqrt{5}+11}=\sqrt{-5+2\sqrt{5}+11}=\sqrt{6+2\sqrt{5}}$

$=\sqrt{{\left(\sqrt{5}\right)}^2+2\cdot \sqrt{5}\cdot 1+1^2}=\sqrt{{\left(\sqrt{5}+1\right)}^2}=\sqrt{5}+1.$

c) Xét biểu thức $\sqrt[3]{x^3+3x^2+3x+1}=\sqrt[3]{{\left(x+1\right)}^3}=x+1.$

Thay x = ‒1 vào biểu thức trên, ta được: ‒1 + 1 = 0.

Thay $x=-\frac{1}{3}$ vào biểu thức trên, ta được: $-\frac{1}{3}+1=\frac{2}{3}.$

Thay $x=\sqrt{2}$ vào biểu thức trên, ta được: $\sqrt{2}+1.$

Lời giải SBT Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số hay khác:

• Bài 25 trang 61 SBT Toán 9 Tập 1: Tìm điều kiện xác định cho mỗi biểu thức sau:a) $\sqrt{x+2024};$....

• Bài 26 trang 61 SBT Toán 9 Tập 1: Điện áp U (V) yêu cầu cho một mạch điện được cho bởi công thức $U=\sqrt{P\cdot R},$ trong đó P (W) là công suất tiêu thụ của điện trở và R (Ω) là giá trị điện trở.....

• Bài 27 trang 61 SBT Toán 9 Tập 1: Tốc độ v (m/s) của một chiếc ca nô được tính theo độ dài đường sóng nước sau đuôi l (m) của ca nô bởi công thức ...

• Bài 28 trang 61 SBT Toán 9 Tập 1: Một chất điểm di chuyển từ đỉnh A’ đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). ....

• Bài 29 trang 61 SBT Toán 9 Tập 1: a) Tìm giá trị nhỏ nhất của biểu thức: $A=5+\sqrt{2x-1}.$...

• Bài 30 trang 62 SBT Toán 9 Tập 1: Tìm x không âm, biết: a) $2\sqrt{x}=14;$....