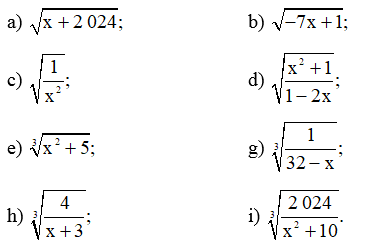Tìm điều kiện xác định cho mỗi biểu thức sau: căn bậc hai (x + 2024)

Tìm điều kiện xác định cho mỗi biểu thức sau:

Giải SBT Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số - Cánh diều

Bài 25 trang 61 SBT Toán 9 Tập 1: Tìm điều kiện xác định cho mỗi biểu thức sau:

Lời giải:

a) Biểu thức $\sqrt{x + 2024}$ xác định khi x + 2 024 ≥ 0 hay x ≥ ‒2 024.

b) Biểu thức $\sqrt{- 7 x + 1}$ xác định khi ‒7x + 1 ≥ 0 hay ‒7x ≥ ‒1, do đó $x \leq \frac{1}{7} .$

c) Biểu thức $\sqrt{\frac{1}{x^{2}}}$ xác định khi $\frac{1}{x^{2}} \geq 0$ và x ≠ 0.

Xét $\frac{1}{x^{2}} \geq 0,$ ta có x² > 0. Điều này xảy ra khi và chỉ khi x ≠ 0.

Vậy $\sqrt{\frac{1}{x^{2}}}$ xác định khi x ≠ 0.

d) Biểu thức $\sqrt{\frac{x^{2} + 1}{1 - 2 x}}$ xác định khi $\frac{x^{2} + 1}{1 - 2 x} \geq 0$ và 1 – 2x ≠ 0.

⦁ Xét $\frac{x^{2} + 1}{1 - 2 x} \geq 0,$ ta có 1 – 2x > 0 (do x² + 1 ≥ 0 với mọi x), hay –2x > –1 nên $x < \frac{1}{2} .$

⦁ Xét 1 – 2x ≠ 0, ta có 2x ≠ 1 hay $x \neq \frac{1}{2} .$

Kết hợp các điều kiện, ta có biểu thức $\sqrt{\frac{x^{2} + 1}{1 - 2 x}}$ xác định khi $x < \frac{1}{2} .$

e) Biểu thức $\sqrt[3]{x^{2} + 5}$ xác định với mọi số thực x vì x² + 5 xác định với mọi số thực x.

g) Biểu thức $\sqrt[3]{\frac{1}{32 - x}}$ xác định khi $\frac{1}{32 - x}$ xác định, hay 32 ‒ x ≠ 0 nên x ≠ 32.

h) Biểu thức $\sqrt[3]{\frac{4}{x + 3}}$ xác định khi $\frac{4}{x + 3}$ xác định, hay x + 3 ≠ 0 nên x ≠ ‒3.

i) Biểu thức $\sqrt[3]{\frac{2 024}{x^{2} + 10}}$ xác định khi $\frac{2 024}{x^{2} + 10}$ xác định.

Với mọi số thực x ta có x² + 10 ≥ 10 nên x² + 10 ≠ 0 với mọi số thực x.

Do đó $\frac{2 024}{x^{2} + 10}$ xác định với mọi số thực x.

Vậy biểu thức $\sqrt[3]{\frac{2 024}{x^{2} + 10}}$ xác định với mọi số thực x.

Lời giải SBT Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số hay khác: