Cho hình thang cân ABCD có AB // CD và AC ⊥ AD. Tính độ dài cạnh AD

Cho hình thang cân ABCD có AB // CD và AC ⊥ AD. Tính độ dài cạnh AD, biết AB = 5 cm và CD = 11 cm.

Giải SBT Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 6 trang 53 SBT Toán 9 Tập 1: Cho hình thang cân ABCD có AB // CD và AC ⊥ AD. Tính độ dài cạnh AD, biết AB = 5 cm và CD = 11 cm.

Lời giải:

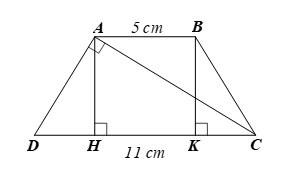
Kẻ AH, BK vuông góc với CD lần lượt tại H, K nên AH ⊥ HK, BK ⊥ HK. Do đó AH // BK.

Do AB // CD, mà H, K ∈ CD nên AB // HK.

Xét tứ giác ABKH có AH // BK và AB // HK nên ABKH là hình bình hành.

Lại có $\hat{A H K} = 90 °$ nên ABKH là hình chữ nhật.

Suy ra AH = BK và HK = AB = 5 cm.

Xét ∆ADH (vuông tại H) và ∆BCK (vuông tại K) có:

AD = BC (do ABCD là hình thang cân), AH = BK.

Do đó ∆ADH = ∆BCK (cạnh huyền – cạnh góc vuông).

Suy ra DH = CK (hai cạnh tương ứng).

Mà DH + HK + CK = CD

Nên $D H = C K = \frac{C D - H K}{2} = \frac{11 - 5}{2} = 3 (cm) .$

Xét ∆ACD và ∆HAD có:

$\hat{D A C} = \hat{D H A} = 90 °$ và $\hat{A C D}$ là góc chung.

Do đó ∆ACD ᔕ ∆HAD (g.g)

Suy ra $\frac{C D}{A D} = \frac{A D}{H D}$ hay AD² = CD.HD.

Vì vậy, $A D = \sqrt{C D \cdot H D} = \sqrt{11 \cdot 3} = \sqrt{33} cm .$

Lời giải SBT Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay khác: