Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A

Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác của góc

Giải sách bài tập Toán 9 Bài tập cuối chương 5 - Chân trời sáng tạo

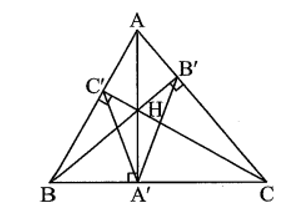
Bài 13 trang 100 sách bài tập Toán 9 Tập 1: Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác của góc $\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}.$

Lời giải:

Gọi H là trực tâm của tam giác ABC.

Do AA’, BB’, CC’ là đường cao ∆ABC nên AA’ ⊥ BC; BB’ ⊥ AC; CC’ ⊥ AB.

Ta có: $\widehat{BC\text{'}H}=\widehat{BA\text{'}H}=90°,$ nên bốn điểm  B, A’, H, C’ cùng nằm trên đường tròn đường kính BH.

Do đó $\widehat{C^{\text{'}}{A}^{\text{'}}H}=\widehat{C^{\text{'}}BH}$ (hai góc nội tiếp cùng chắn cung C’H).

Chứng minh tương tự, ta cũng có $\widehat{B\text{'}A\text{'}H}=\widehat{B\text{'}CH}.$

Mà $\widehat{C\text{'}BH}=\widehat{B\text{'}CH}$  (cùng phụ với $\widehat{BAC}\text{)},$> nên ta có $\widehat{C\text{'}A\text{'}H}=\widehat{B\text{'}A\text{'}H}.$

Vậy A’A là tia phân giác của góc $\widehat{B\text{'}A\text{'}C\text{'}}.$

Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:

• Câu 1 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc $\widehat{BAC}$ trong Hình 1 là...

• Câu 2 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc $\widehat{BAC}$ trong Hình 2 là...

• Câu 3 trang 98 sách bài tập Toán 9 Tập 1: Cho biết $\text{sđ}\stackrel{⏜}{AB}=\text{sđ}\stackrel{⏜}{BC}=\text{sđ}\stackrel{⏜}{CA}$ và OB = R. Độ dài cạnh BC là...

• Câu 4 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 4....

• Câu 5 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 5. ...

• Câu 6 trang 99 sách bài tập Toán 9 Tập 1: Số đo θ của $\widehat{RBS}$ có trong Hình 6 là...

• Câu 7 trang 99 sách bài tập Toán 9 Tập 1: Cung 50° của một đường tròn đường kính d = 25 cm có độ dài (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là...

• Câu 8 trang 99 sách bài tập Toán 9 Tập 1: Hình quạt tròn bán kính R = 100 cm ứng với cung 40° có diện tích (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là...

• Câu 9 trang 99 sách bài tập Toán 9 Tập 1: Hình vành khuyên giới hạn bởi hai đường tròn (O; 5 cm) và (O; 2 cm) có diện tích (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là...

• Câu 10 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho hai đường tròn C(O; 7 cm), C’(O’; 8 cm) và OO’ = 15 cm....

• Câu 11 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho bốn điểm A, B, C, D trên đường tròn (O) như Hình 7....

• Câu 12 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho AB và AC là hai tiếp tuyến tiếp xúc với đường tròn (O; R) lần lượt tại hai tiếp điểm B và C (Hình 8)....

• Bài 14 trang 100 sách bài tập Toán 9 Tập 1: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau ...

• Bài 15 trang 100 sách bài tập Toán 9 Tập 1: Cho tam giác ABC cân tại A, $\widehat{A}<90°.$ Vẽ đường tròn đường kính AB cắt BC và AC lần lượt tại D và E. Chứng minh rằng...

• Bài 16 trang 101 sách bài tập Toán 9 Tập 1: Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH...

• Bài 17 trang 101 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại hai điểm A và B phân biệt. Vẽ đường thẳng vuông góc với AB tại A và cắt (O), ...

• Bài 18 trang 101 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M cắt đường tròn (O) tại hai điểm B, C...