Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M
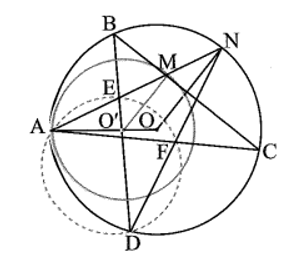
Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M cắt đường tròn (O) tại hai điểm B, C. Đường thẳng BO’ cắt đường tròn (O) tại điểm thứ hai D và cắt đường thẳng AM tại E. Gọi F là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADE với AC và N là giao điểm thứ hai của AN với (O). Chứng minh rằng:
Giải sách bài tập Toán 9 Bài tập cuối chương 5 - Chân trời sáng tạo
Bài 18 trang 101 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M cắt đường tròn (O) tại hai điểm B, C. Đường thẳng BO’ cắt đường tròn (O) tại điểm thứ hai D và cắt đường thẳng AM tại E. Gọi F là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADE với AC và N là giao điểm thứ hai của AN với (O). Chứng minh rằng:
a) O’M // ON.
b) Ba điểm D, N, F thẳng hàng.
c) DF là tia phân giác của góc
Lời giải:
a) Xét ∆O’AM cân tại O’ (do O’A = O’M) nên
Xét ∆OAN cân tại O (do OA = ON) nên
Do đó mà hai góc này ở vị trí đồng vị, suy ra O’M // ON.
b) Do BC là tiếp tuyến của (O’) nên O’M ⊥ BC.
Mà O’M // ON nên ON ⊥ BC.
Xét ∆OBC cân tại O (do OB = OC) nên đường cao ON đồng thời là đường phân giác của tam giác, hay do đó hay N là điểm chính giữa cung BC.
Mặt khác (hai góc nội tiếp cùng chắn cung NC của đường tròn (O)) và (góc nội tiếp chắn cung BN của đường tròn (O))
Do đó (1)
Trong đường tròn ngoại tiếp tam giác ADE, ta có:
(góc nội tiếp cùng chắn cung EF). (2)
Từ (1), (2) ta có suy ra D, N, F thẳng hàng.
c) Ta có hai cung BN và NC có số đo bằng nhau, suy ra (hai góc nội tiếp chắn hai cung bằng nhau) hay DF là tia phân giác của
Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:
Câu 1 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc trong Hình 1 là...
Câu 2 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc trong Hình 2 là...
Câu 3 trang 98 sách bài tập Toán 9 Tập 1: Cho biết và OB = R. Độ dài cạnh BC là...
Câu 4 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 4....
Câu 5 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 5. ...
Câu 6 trang 99 sách bài tập Toán 9 Tập 1: Số đo θ của có trong Hình 6 là...