Cho tam giác ABC cân tại A, góc A < 90 độ Vẽ đường tròn đường kính AB cắt BC

Cho tam giác ABC cân tại A, $\widehat{A}<90°.$ Vẽ đường tròn đường kính AB cắt BC và AC lần lượt tại D và E. Chứng minh rằng:

Giải sách bài tập Toán 9 Bài tập cuối chương 5 - Chân trời sáng tạo

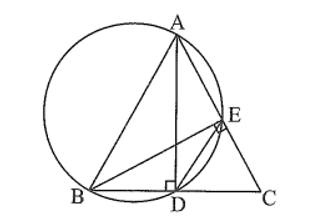
Bài 15 trang 100 sách bài tập Toán 9 Tập 1: Cho tam giác ABC cân tại A, $\widehat{A}<90°.$ Vẽ đường tròn đường kính AB cắt BC và AC lần lượt tại D và E. Chứng minh rằng:

a) ∆DBE là tam giác cân.

b) $\widehat{CBE}=\frac{1}{2}\widehat{BAC}.$

Lời giải:

a) Ta có D, E cùng nằm trên đường tròn đường kính AB nên $\widehat{ADB}=\widehat{AEB}=90°$ hay AD ⊥ BC và BE ⊥ AC.

Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó D là trung điểm BC, suy ra $DB=DC=\frac{1}{2}BC.$

Xét ∆BEC vuông tại E có ED là đường trung tuyến ứng với cạnh huyền BC nên $ED=\frac{1}{2}BC.$

Do đó DE = DB = DC.

Vậy ∆BDE cân tại D.

b) Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là tia phân giác của $\widehat{BAC},$ do đó $\widehat{BAD}=\frac{1}{2}\widehat{BAC}.$

Ta có $\widehat{DBE}=\widehat{DEB}$ (do ∆BDE cân tại D) và $\widehat{BAD}=\widehat{BED}$ (hai góc nội tiếp cùng chắn cung BD).

Suy ra $\widehat{DBE}=\frac{1}{2}\widehat{BAC}$ hay $\widehat{CBE}=\frac{1}{2}\widehat{BAC}.$

Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:

• Câu 1 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc $\widehat{BAC}$ trong Hình 1 là...

• Câu 2 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc $\widehat{BAC}$ trong Hình 2 là...

• Câu 3 trang 98 sách bài tập Toán 9 Tập 1: Cho biết $\text{sđ}\stackrel{⏜}{AB}=\text{sđ}\stackrel{⏜}{BC}=\text{sđ}\stackrel{⏜}{CA}$ và OB = R. Độ dài cạnh BC là...

• Câu 4 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 4....

• Câu 5 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 5. ...

• Câu 6 trang 99 sách bài tập Toán 9 Tập 1: Số đo θ của $\widehat{RBS}$ có trong Hình 6 là...

• Câu 7 trang 99 sách bài tập Toán 9 Tập 1: Cung 50° của một đường tròn đường kính d = 25 cm có độ dài (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là...

• Câu 8 trang 99 sách bài tập Toán 9 Tập 1: Hình quạt tròn bán kính R = 100 cm ứng với cung 40° có diện tích (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là...

• Câu 9 trang 99 sách bài tập Toán 9 Tập 1: Hình vành khuyên giới hạn bởi hai đường tròn (O; 5 cm) và (O; 2 cm) có diện tích (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là...

• Câu 10 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho hai đường tròn C(O; 7 cm), C’(O’; 8 cm) và OO’ = 15 cm....

• Câu 11 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho bốn điểm A, B, C, D trên đường tròn (O) như Hình 7....

• Câu 12 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho AB và AC là hai tiếp tuyến tiếp xúc với đường tròn (O; R) lần lượt tại hai tiếp điểm B và C (Hình 8)....

• Bài 13 trang 100 sách bài tập Toán 9 Tập 1: Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác ...

• Bài 14 trang 100 sách bài tập Toán 9 Tập 1: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau ...

• Bài 16 trang 101 sách bài tập Toán 9 Tập 1: Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH...

• Bài 17 trang 101 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại hai điểm A và B phân biệt. Vẽ đường thẳng vuông góc với AB tại A và cắt (O), ...

• Bài 18 trang 101 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M cắt đường tròn (O) tại hai điểm B, C...