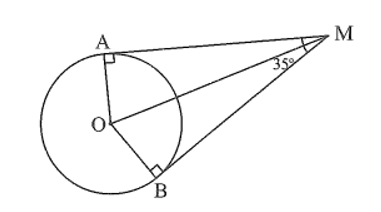
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và góc AMB = 35 độ

Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và

Giải sách bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp - Chân trời sáng tạo

Bài 3 trang 92 sách bài tập Toán 9 Tập 1: Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và $\hat{A M B} = 35 ° .$

a) Tính số đo của góc ở tâm tạo bởi hai bán kính OA, OB.

b) Tính số đo mỗi cung $\overset{⏜}{A B}$ (cung lớn và cung nhỏ).

Lời giải:

Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và góc AMB = 35 độ

a) Vì MA, MB là hai tiếp tuyến của (O) nên OA ⊥ AM; OB ⊥ BM.

Suy ra $\hat{O A M} = 90 °, \hat{O B M} = 90 ° .$

Xét tứ giác AOBM, ta có:

$\hat{O A M} + \hat{O B M} + \hat{A M B} + \hat{A O B} = 360 °$

Suy ra $90 ° + 90 ° + 35 ° + \hat{A O B} = 360 °$

Do đó $\hat{A O B} = 360 ° - 90 ° - 90 ° - 35 ° = 145 ° .$

b) Vì $\hat{A O B} = 145 °$ nên số đo cung nhỏ AB là 145° và số đo cung lớn AB là:

360° – 145° = 215°.

Lời giải SBT Toán 9 Bài 3: Góc ở tâm, góc nội tiếp hay khác: