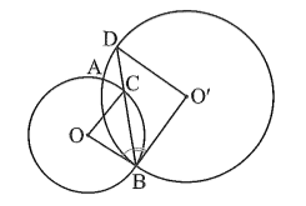
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh và
Giải sách bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp - Chân trời sáng tạo
Bài 4 trang 93 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh và
Lời giải:
Ta có (vì BC là đường phân giác của (1)
Do B, C thuộc đường tròn (O) nên OB = OC, suy ra ∆OBC cân tại O, do đó (2)
Do B, D thuộc đường tròn (O’) nên O’B = O’D, suy ra ∆O’BD cân tại O’, do đó (3)
Từ (1), (2) và (3) suy ra
Mặt khác, và
Do đó
Lời giải SBT Toán 9 Bài 3: Góc ở tâm, góc nội tiếp hay khác: