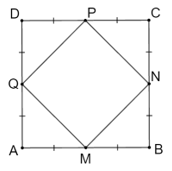
Cho hình vuông ABCD có cạnh bằng 4 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA

Cho hình vuông ABCD có cạnh bằng 4 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính, chu vi của đường tròn đó.

Giải sách bài tập Toán 9 Bài 29: Tứ giác nội tiếp - Kết nối tri thức

Bài 9.28 trang 56 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 4 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính, chu vi của đường tròn đó.

Lời giải:

Do tam giác QAM vuông cân tại A nên ta có

$QM=\sqrt{Q{A}^2+M{A}^2}=\sqrt{2}QA=2\sqrt{2}$(cm)

Tương tự ta có $MN=NP=PQ=QM=2\sqrt{2}$cm.

Suy ra MNPQ là hình thoi.

Mà $\widehat{MNP}=180°-\widehat{MNB}-\widehat{PNC}=180°-45°-45°=90°$

Vì MNPQ là hình vuông có cạnh bằng $2\sqrt{2}$cm và có đường chéo $MP=\sqrt{M{Q}^2+Q{P}^2}=\sqrt{{\left(2\sqrt{2}\right)}^2+{\left(2\sqrt{2}\right)}^2}=4$ (cm).

Vì vậy MNPQ nội tiếp một đường tròn có tâm là trung điểm của MP (dpcm) và có bán kính bằng $\frac{MP}{2}=\frac{4}{2}=2$(cm).

Chu vi của đường tròn đó là $C=2\pi .2=4\pi \approx \mathrm{12,56}$(cm).

Vậy bán kính đường tròn ngoại tiếp tứ giác MNPQ là 2 cm và chu vi đường tròn đó là khoảng 12,56 cm.

Lời giải SBT Toán 9 Bài 29: Tứ giác nội tiếp hay khác:

• Bài 9.21 trang 55 sách bài tập Toán 9 Tập 2: Hãy cho biết số đo các góc còn lại của tứ giác nội tiếp ABCD trong mỗi trường hợp sau: ...

• Bài 9.22 trang 55 sách bài tập Toán 9 Tập 2: Hãy cho biết số đo các góc của tứ giác ABCD nội tiếp đường tròn (O) trong mỗi trường hợp sau: ...

• Bài 9.23 trang 55 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm E ...

• Bài 9.24 trang 56 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm K, hai đường chéo AC và BD cắt nhau tại điểm H ...

• Bài 9.25 trang 56 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm I. Chứng minh rằng ...

• Bài 9.26 trang 56 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm J. Chứng minh rằng ...

• Bài 9.27 trang 56 sách bài tập Toán 9 Tập 2: Chứng minh rằng. Nếu một hình bình hành nội tiếp một đường tròn thì hình đó phải là hình chữ nhật; ...

• Bài 9.29 trang 56 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 3 cm và nội tiếp đường tròn (O) như Hình 9.8 ...

• Bài 9.30 trang 56 sách bài tập Toán 9 Tập 2: Cho hình thoi ABCD có AC = 8 cm, BD = 4 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA ...

• Bài 9.31 trang 56 sách bài tập Toán 9 Tập 2: Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB = 3 cm; AD = 4 cm. Vẽ một hình vuông nội tiếp (O) ...

• Bài 9.32 trang 57 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y ...