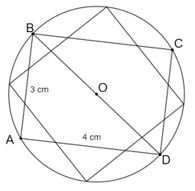
Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB = 3 cm; AD = 4 cm. Vẽ một hình vuông nội tiếp (O)

Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB = 3 cm; AD = 4 cm. Vẽ một hình vuông nội tiếp (O). Tính diện tích của hình vuông đó.

Giải sách bài tập Toán 9 Bài 29: Tứ giác nội tiếp - Kết nối tri thức

Bài 9.31 trang 56 sách bài tập Toán 9 Tập 2: Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB = 3 cm; AD = 4 cm. Vẽ một hình vuông nội tiếp (O). Tính diện tích của hình vuông đó.

Lời giải:

Độ dài đường chéo hình chữ nhật ABCD là:

$BD=\sqrt{A{B}^2+A{D}^2}=\sqrt{3^2+4^2}=5$ (cm)

Đường tròn (O) có tâm O là trung điểm của BD và bán kính là:

$R=\frac{BD}{2}=\frac{5}{2}=\mathrm{2,5}$ (cm)

Hình vuông nội tiếp (O) có cạnh bằng a, đường chéo của hình vuông đó là: $\sqrt{a^2+a^2}=\sqrt{2}a$

Đường tròn (O) ngoại tiếp hình vuông nên ta có:

$R=\frac{a\sqrt{2}}{2}$ hay $\mathrm{2,5}=\frac{a\sqrt{2}}{2}$, suy ra $a=\frac{5\sqrt{2}}{2}$(cm).

Vậy diện tích của hình vuông là: $a^2={\left(\frac{5\sqrt{2}}{2}\right)}^2=\mathrm{12,5}$(cm²).

Lời giải SBT Toán 9 Bài 29: Tứ giác nội tiếp hay khác:

• Bài 9.21 trang 55 sách bài tập Toán 9 Tập 2: Hãy cho biết số đo các góc còn lại của tứ giác nội tiếp ABCD trong mỗi trường hợp sau: ...

• Bài 9.22 trang 55 sách bài tập Toán 9 Tập 2: Hãy cho biết số đo các góc của tứ giác ABCD nội tiếp đường tròn (O) trong mỗi trường hợp sau: ...

• Bài 9.23 trang 55 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm E ...

• Bài 9.24 trang 56 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm K, hai đường chéo AC và BD cắt nhau tại điểm H ...

• Bài 9.25 trang 56 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm I. Chứng minh rằng ...

• Bài 9.26 trang 56 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm J. Chứng minh rằng ...

• Bài 9.27 trang 56 sách bài tập Toán 9 Tập 2: Chứng minh rằng. Nếu một hình bình hành nội tiếp một đường tròn thì hình đó phải là hình chữ nhật; ...

• Bài 9.28 trang 56 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 4 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA ...

• Bài 9.29 trang 56 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 3 cm và nội tiếp đường tròn (O) như Hình 9.8 ...

• Bài 9.30 trang 56 sách bài tập Toán 9 Tập 2: Cho hình thoi ABCD có AC = 8 cm, BD = 4 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA ...

• Bài 9.32 trang 57 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y ...