Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F
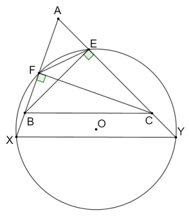
Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y. Chứng minh rằng XY song song với BC.
Giải sách bài tập Toán 9 Bài 29: Tứ giác nội tiếp - Kết nối tri thức
Bài 9.32 trang 57 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y. Chứng minh rằng XY song song với BC.
Lời giải:
Vì các tam giác vuông BED và BFC có chung cạnh huyền BC nên bốn điểm B, F, E, C cùng nằm trên đường tròn đường kính BC.
Do đó BFEC là tứ giác nội tiếp đường tròn bán kính BC.
Vì tổng các góc đối nhau của các tứ giác nội tiếp BFEC và XFEY bằng 180° nên ta có:
Do đó BC // XY (do hai góc đồng vị bằng nhau).
Lời giải SBT Toán 9 Bài 29: Tứ giác nội tiếp hay khác: