Bất phương trình mx^2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi
Câu hỏi:
Bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi
B. ;
C. ;
D. .
Trả lời:
Đáp án đúng là: D
+) Khi m = 0, ta có:
mx2 – (2m – 1)x + m + 1 < 0
⇔ x + 1 < 0
⇔ x < –1
Do đó, m = 0 không thỏa mãn yêu cầu đề bài
+) Khi m ≠ 0, ta có:
Xét tam thức: f(x) = mx2 – (2m – 1)x + m + 1 có:
a = m,
∆ = [–(2m – 1)2] – 4.m.(m + 1) = 4m2 – 4m + 1 – 4m2 – 4m = –8m + 1
Để mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi mx2 – (2m – 1)x + m + 1 ≥ 0 với mọi số thực x
Vậy khi thì bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm.
Xem thêm bài tập Toán 10 CD có lời giải hay khác:
Câu 1:
Cho hàm số y = với m là tham số. Tìm m để hàm số xác định trên (0; 1).
Xem lời giải »
Câu 2:
Xác định parabol y = ax2 + bx + c (a ≠ 0), biết rằng parabol đó đi qua điểm A(8; 0) và có đỉnh là I(6; 12).
Xem lời giải »
Câu 3:
Để phương trình |x + 3|(x – 2) + m – 1 = 0 có đúng một nghiệm, các giá trị của tham số m là:
Xem lời giải »
Câu 4:
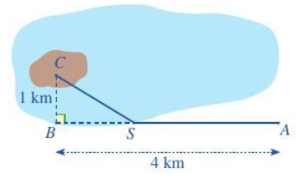
Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như hình dưới đây. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 4 triệu đồng và 6 triệu đồng. Biết tổng số tiền công là 25 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
Xem lời giải »

