Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây đúng?

Cho tam giác​​ ABC​​ có trực tâm​​ H. Gọi​​ D​​ là điểm đối xứng với​​ B​​ qua tâm​​ O​​ của đường tròn ngoại tiếp tam giác​​ ABC. Khẳng định nào sau đây đúng?

A. $\overrightarrow{AH}$  = $\overrightarrow{CD}$ ;

Đáp án đúng là: C

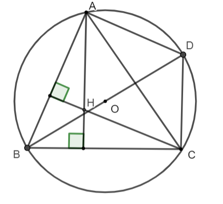
Ta có: AH ⊥ BC (H là trực tâm tam giác ABC) và DC ⊥ BC (do góc $\widehat{DCB}$  chắn nửa đường tròn)

Þ AH // DC (1)

Ta có: CH ⊥ AB (H là trực tâm tam giác ABC) và DA ⊥ AB ( do góc $\widehat{BAD}$  chắn nửa đường tròn)

Þ CH // DA (2)

Từ (1) và (2) suy ra tứ giác ADCH là hình bình hành

Do đó $\overrightarrow{AH}$=$\overrightarrow{DC}$và $\overrightarrow{AD}$= $\overrightarrow{HC}$.